Properties of a One-To-One Function
A one-to-one function, also called an injective function, never maps distinct elements of its domain to the same element of its co-domain. In other words, every element of the function's range corresponds to exactly one element of its domain. Occasionally, an injective function from
An easy way to check if a function is a one-to-one is by graphing it and then performing the horizontal line test. If any horizontal line intersects the graph at more than one point, the function is not one-to-one. To see this, note that the points of intersection have the same y-value, because they lie on the line, but different x values, which by definition means the function cannot be one-to-one.
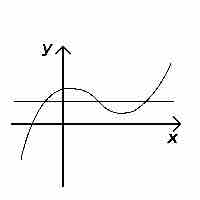
Horizontal Line Test
Because the horizontal line crosses the graph of the function more than once, it fails the horizontal line test and cannot be one-to-one.
Determining If a Function is One-To-One
Example 1: Is the function $f(x)={x}^{2}$ (with no domain restrictions) one-to-one?
One way to check if the function is one-to-one is to graph the function and perform the horizontal line test. The graph below shows that it forms a parabola and fails the horizontal line test.
Parabola Graph
The graph of the function
Another way to determine if the function is one-to-one is to make a table of values and check to see if every element of the range corresponds to exactly one element of the domain. A list of ordered pairs for the function are:
The ordered pairs
Example 2: Is the function $f(x)=\left | x-2 \right |$ one-to-one?
This is an absolute value function, which is graphed below. Notice it fails the horizontal line test. Because each unique input does not have a unique output, this function cannot be one-to-one.
Absolute Value Graph
The graph of the function,