Overview of $e^{x}$
The basic exponential function, sometimes referred to as the exponential function, is
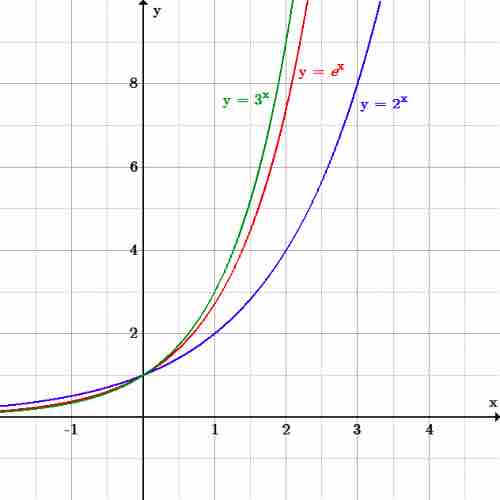
The graphs of $2^x$ , $e^x$ , and $3^x$
The graph of
The graph of
A Model For Proportional Change
The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change (i.e., percentage increase or decrease) in the dependent variable. If the change is positive, this is called exponential growth and if it is negative, it is called exponential decay. For example, because a radioactive substance decays at a rate proportional to the amount of the substance present, the amount of the substance present at a given time can be modeled with an exponential function. Also, because the the growth rate of a population of bacteria in a petri dish is proportional to its size, the number of bacteria in the dish at a given time can be modeled by an exponential function such as