In mathematics, a parabola is a conic section, created from the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface. In other words, the plane is at the same angle as the outside surface of the cone.

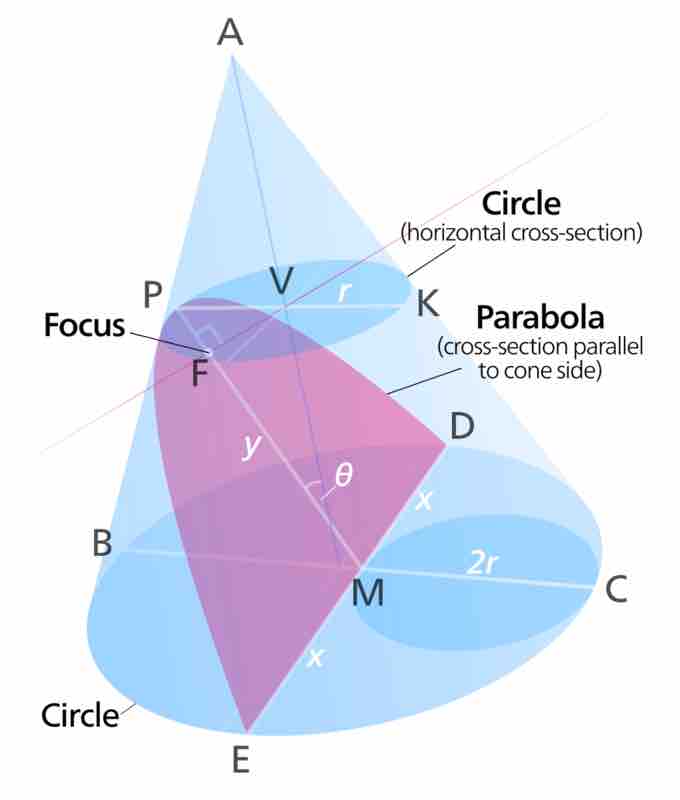
Parabolic conic section

This diagram shows how a parabola is generated by the intersection of a plane with a right circular cone. It also shows the $y$ and $x$ axes that would be used to view the parabola on a coordinate graph. The vertex of the parabola here is point $P$, and the diagram shows the radius $r$ between that point and the cone's central axis, as well as the angle $\theta$ between the parabola's axis of symmetry and the cone's central axis. 

All parabolas have the same set of basic features. The axis of symmetry is a line that is at the same angle as the cone and divides the parabola in half.

Vertex

The vertex is the point where the plane intersects the exterior surface of the cone. It forms the rounded end of the parabola. The vertex is therefore also a point on the cone, and the distance between that point and the cone's central axis is the radius of a circle.

Focus

In the diagram showing the parabolic conic section, a red line is drawn from the center of that circle to the axis of symmetry, so that a right angle is formed. The point on the axis of symmetry where the right angle is located is called the focus. By doing this, a right triangle is created.

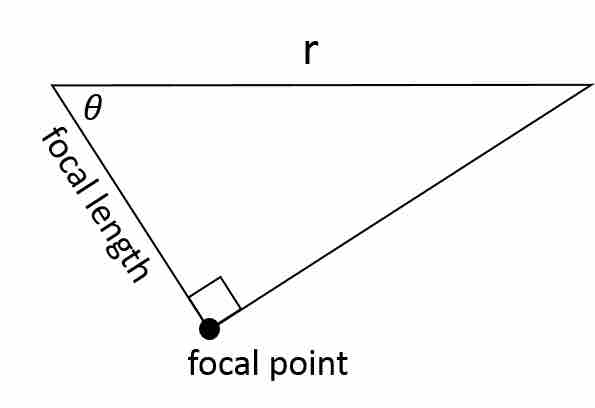
Right triangle

A right triangle is formed from the focal point of the parabola.

The focal length is the leg of the right triangle that exists along the axis of symmetry, and the focal point is the vertex of the right triangle. Using the definition of sine as opposite over hypotenuse, we can find a formula for the focal length "$f$" in terms of the radius and the angle:

$\displaystyle{ \begin{aligned} \sin(\theta) &= \frac{f}{r} \\ f &= r\sin(\theta) \end{aligned} }$

Directrix

All parabolas have a directrix. The directrix is a straight line on the opposite side of the parabolic curve from the focus. The parabolic curve itself is the set of all points that are equidistant (equal distances) from both the directrix line and the focus.

Features of Parabolas

On a coordinate plane, parabolas are frequently encountered as graphs of quadratic functions, such as: 

$y=x^2$

Parabolas can open up, down, left, right, or in some other arbitrary direction. Any parabola can be repositioned and rescaled to fit exactly on any other parabola—that is, all parabolas are similar.

To locate the $x$-coordinate of the vertex, cast the equation for $y$ in terms of $a x^2 + b x + c$. The vertex will be at the point:

$\displaystyle{x= \frac{-b}{2a}}$

For example, in the parabola $y=x^2$, $a=1$, $b=0$, $c=0$, and the vertex is at $x=0$.

Parabolas have the property that, if they are made of material that reflects light, then light which enters a parabola traveling parallel to its axis of symmetry is reflected to its focus. This happens regardless of where on the parabola the reflection occurs. Conversely, light that originates from a point source at the focus is reflected, or collimated, into a parallel beam. The light leaves the parabola parallel to the axis of symmetry. The same effect occurs with sound and other forms of energy. This reflective property is the basis of many practical uses of parabolas.

The parabola has many important applications, from the design of automobile headlight reflectors to calculating the paths of ballistic missiles. They are frequently used in physics, engineering, and other sciences.