A hyperbola is one of the four conic sections. All hyperbolas share common features, and it is possible to determine the specifics of any hyperbola from the equation that defines it.
Standard Form
Diagram of a hyperbola
All hyperbolas share common features.
If the foci lie on the
If the foci lie on the
We will use the
Center
The center has coordinates
Vertices
The vertices have coordinates
Co-Vertices
The co-vertices correspond to
Asymptotes
The major and minor axes
The rectangle itself is also useful for drawing the hyperbola graph by hand, as it contains the vertices. When drawing the hyperbola, draw the rectangle first. Then draw in the asymptotes as extended lines that are also the diagonals of the rectangle. Finally, draw the curve of the hyperbola by following the asymptote inwards, curving in to touch the vertex on the rectangle, and then following the other asymptote out. Repeat for the other branch.
Focal Points
The foci have coordinates
Rectangular Hyperbola
Rectangular hyperbolas, defined by
for some constant
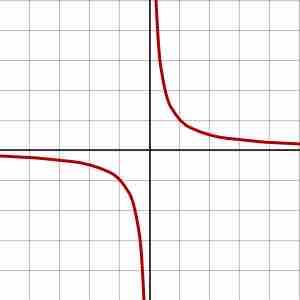
Rectangular hyperbola
This rectangular hyperbola has its center at the origin, and is also the graph of the function
Center
The center of a rectangular hyperbola has coordinates
Vertices and Co-Vertices
The rectangular hyperbola is highly symmetric. Both its major and minor axis values are equal, so that
The co-vertices have coordinates
Asymptotes
The asymptotes of a rectangular hyperbola are the
Focal Points
We can use