Equation of an Ellipse

An ellipse is a conic section, formed by the intersection of a plane with a right circular cone. The standard form for the equation of the ellipse is:

$\displaystyle{\frac{\left(x-h\right)^2}{a^2} + \frac{\left(y-k\right)^2}{b^2} = 1}$

if the ellipse is oriented horizontally, and:

$\displaystyle{\frac{\left(y-k\right)^2}{a^2} + \frac{\left(x-h\right)^2}{b^2} = 1}$

if the ellipse is oriented vertically. We will use the horizontal case to demonstrate how to determine the properties of an ellipse from its equation, so that $a$ is associated with x-coordinates, and $b$ with y-coordinates. For a vertical ellipse, the association is reversed.

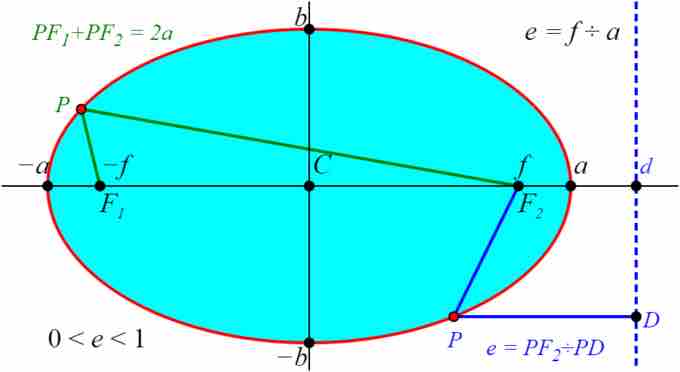
Diagram of an ellipse

This diagram of a horizontal ellipse shows the ellipse itself in red, the center $C$ at the origin, the focal points at $\left(+f,0\right)$ and $\left(-f,0\right)$, the major axis vertices at $\left(+a,0\right)$ and $\left(-a,0\right)$, the minor axis vertices at $\left(0,+b\right)$ and $\left(0,-b\right)$. It also shows how the sum of the distances from any point on the ellipse to the two foci is a constant, and how the eccentricity is determined by relating one of the foci to a line $D$ called the directrix.

Parts of an Ellipse

Center

The center of the ellipse has coordinates $(h,k)$.

Major Axis

The major axis of the ellipse is the longest width across it. For a horizontal ellipse, that axis is parallel to the $x$-axis. The major axis has length $2a$. Its endpoints are the major axis vertices, with coordinates $(h \pm a, k)$.

Minor Axis

The minor axis of the ellipse is the shortest width across it. For a horizontal ellipse, it is parallel to the $y$-axis. The minor axis has length $2b$. Its endpoints are the minor axis vertices, with coordinates $(h, k \pm b)$.

Foci

The foci are two points inside the ellipse that characterize its shape and curvature. For a horizontal ellipse, the foci have coordinates $(h \pm c,k)$, where the focal length $c$ is given by

$c^2 = a^2 - b^2$

Eccentricity

All conic sections have an eccentricity value, denoted $e$. All ellipses have eccentricities in the range $0 \leq e < 1$. An eccentricity of zero is the special case where the ellipse becomes a circle. An eccentricity of $1$ is a parabola, not an ellipse.

The eccentricity is defined as:

$\displaystyle{e = \frac{c}{a}}$

or, equivalently:

$\displaystyle{ \begin{aligned} e &= \frac{\sqrt{a^2 - b^2}}{a} \\ &= \sqrt{ \frac{a^2 - b^2}{a^2} } \\ &= \sqrt{ 1 - \frac{b^2}{a^2}} \end{aligned} }$

The orbits of the planets and their moons are ellipses with very low eccentricities, which is to say they are nearly circular. The orbits of comets around the sun can be much more eccentric. For comets and planets, the sun is located at one focus of their elliptical orbits.