Introduction
Probability uses the mathematical ideas of sets, as we have seen in the definition of both the sample space of an experiment and in the definition of an event. In order to perform basic probability calculations, we need to review the ideas from set theory related to the set operations of union, intersection, and complement.
Union
The union of two or more sets is the set that contains all the elements of each of the sets; an element is in the union if it belongs to at least one of the sets. The symbol for union is
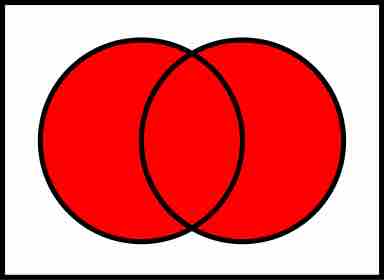
Union of Two Sets
The shaded Venn Diagram shows the union of set
In symbols, since the union of
For example, if
Where
If sets
This can even be extended to more sets if they are all disjoint:
Intersection
The intersection of two or more sets is the set of elements that are common to each of the sets. An element is in the intersection if it belongs to all of the sets. The symbol for intersection is

Intersection of Two Sets
Set
In mathematical notation, the intersection of
When events are independent, meaning that the outcome of one event doesn't affect the outcome of another event, we can use the multiplication rule for independent events, which states:
For example, let's say we were tossing a coin twice, and we want to know the probability of tossing two heads. Since the first toss doesn't affect the second toss, the events are independent. Say is the event that the first toss is a heads and