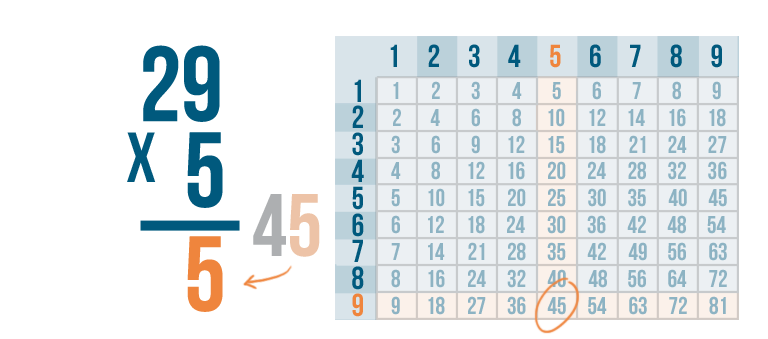Using Carrying
On the last page, you practiced multiplying vertically stacked numbers. Some problems need an extra step. For example, can you multiply the numbers in this expression?
If you tried to multiply 9 x 5, you might have noticed that there was no room to write the product, 45. When the product of two numbers is greater than 9, you'll need to use a technique called carrying. If you know how to add large numbers, you might remember using carrying in addition too. Let's see how it works in multiplication.
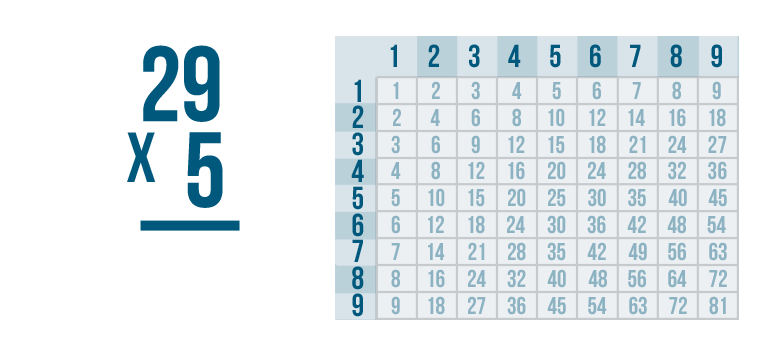
Let's try the problem we just looked at, 29 x 5.

As usual, we'll start by multiplying the 5 by the top-right digit, 9.

According to our times table, 5 x 9 is 45, but there's no room to write both digits underneath the 5 and 9.
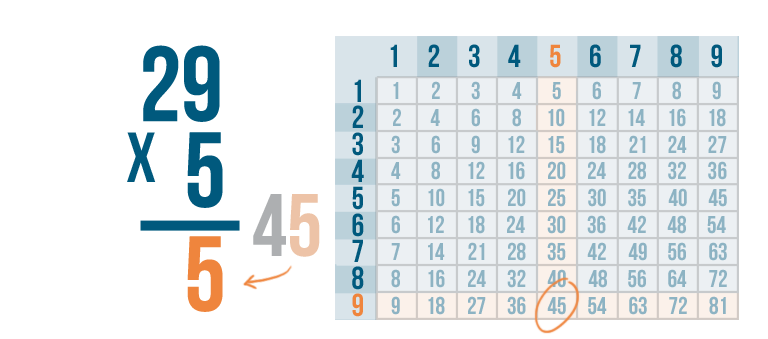
We'll write the right digit, 5, under the line...
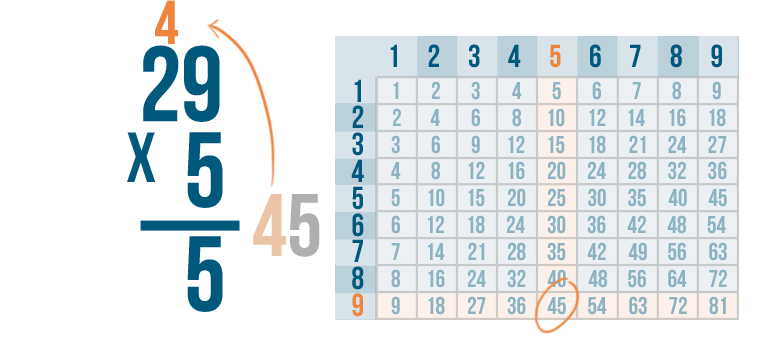
We'll write the right digit, 5, under the line...then we'll carry the left digit, 4, up to the next set of digits in the problem.

See how it works? We multiplied 5 and 9 to get 45. We put the 5 underneath the line, carried the 4 and placed it above the next set of digits.
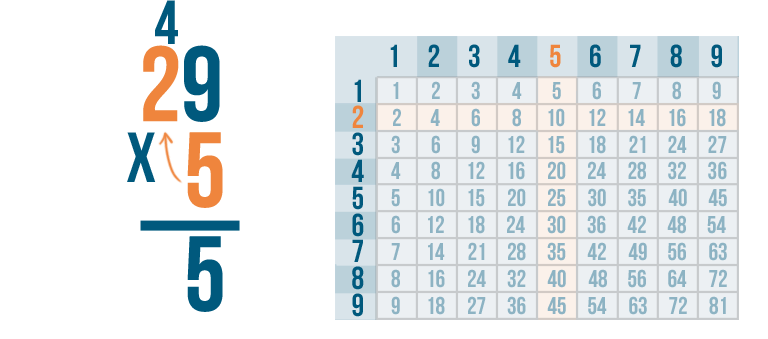
Now it's time for the next step. It's the same as with any other multiplication problem. We'll multiply 5 x 2.

5 x 2 = 10. However, we won't write 10 under the line yet - there's one more step.
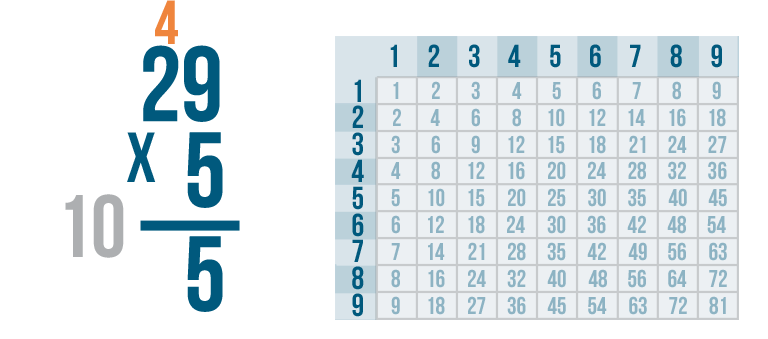
Remember the number we carried, 4?
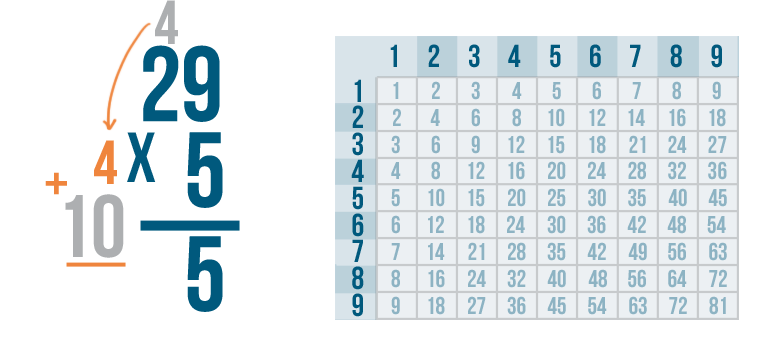
We have to add it to our product, 10.
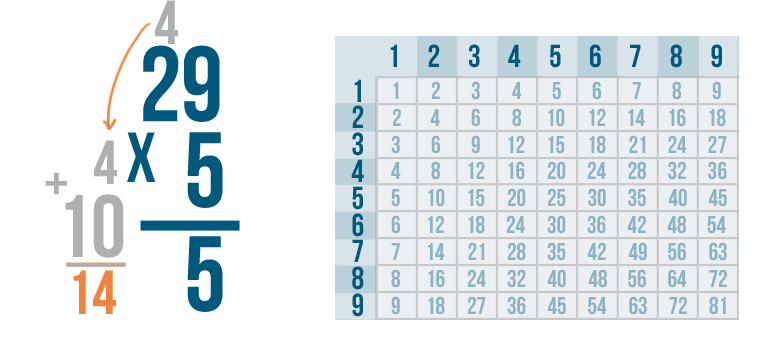
4 + 10 is 14.
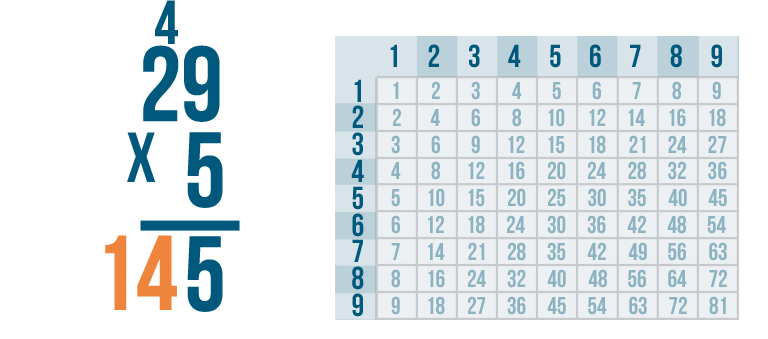
We'll write 14 beneath the line.
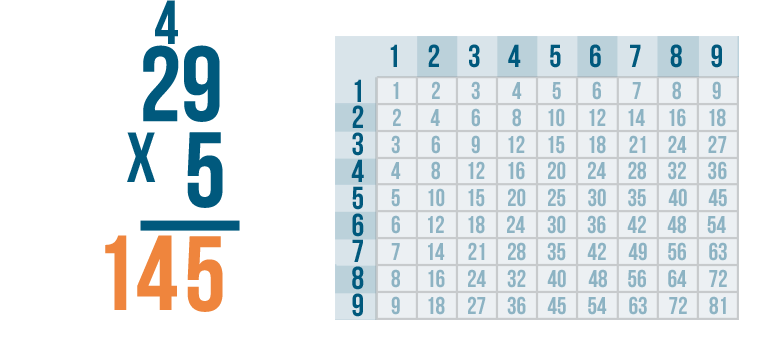
Our total is 145. We now know that 29 x 5 = 145.

Let's try another problem, just for practice. 208 x 6.

First, we multiply the bottom number, 6, by the digit on the top right. That's 8.

6 x 8 is 48.

We'll write the 8 under the line...
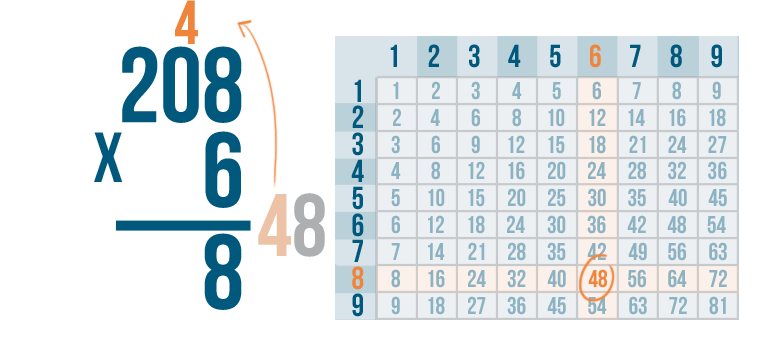
We'll write the 8 under the line...and carry the 4. We'll place it above the next digit.

The next digit is 0.

Anything times zero is 0, so we know that 7 x 0 = 0.

Remember, we don't write that 0 beneath the line yet. We have to add it to the 4 we just carried.

4 + 0 = 4. We'll write 4 beneath the line.

Finally, we multiply 6 and 2.

6 x 2 = 12, so we'll write 12 beneath the line.

We're done! The answer is 1248, or one thousand, two hundred and forty-eight. 208 x 6 = 1248.
-
Now you try it. See if you can solve these problems. Remember, you can always use your times table for help.