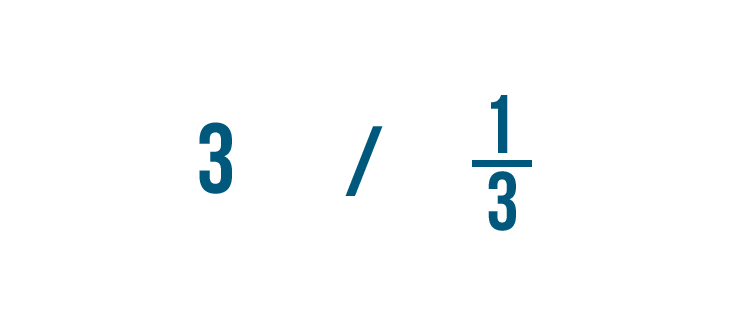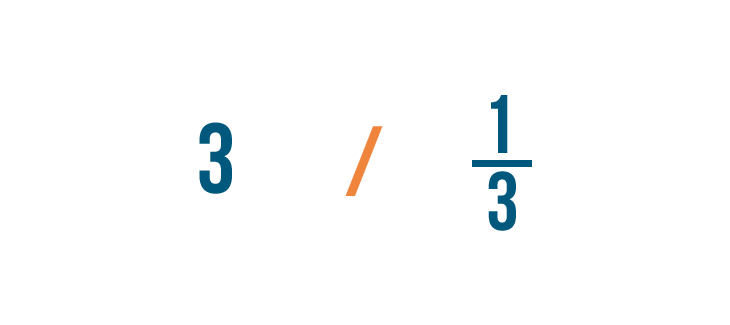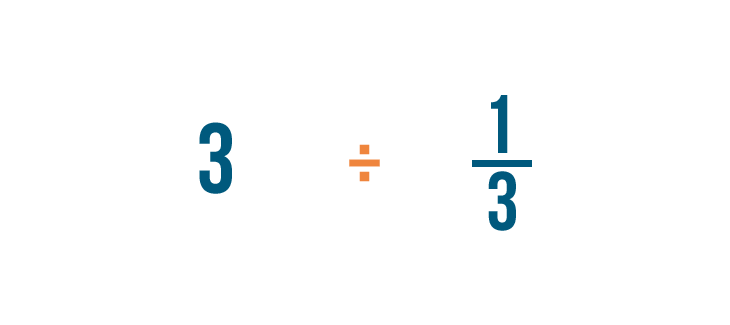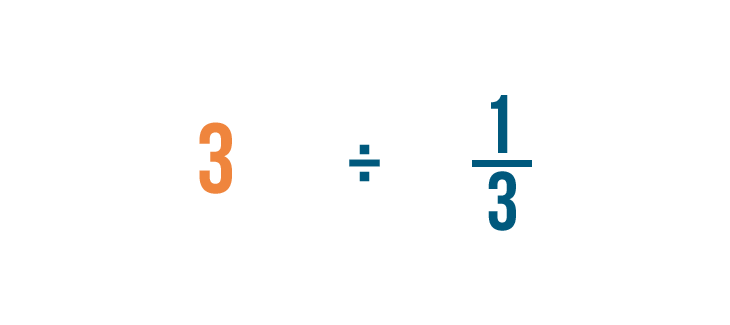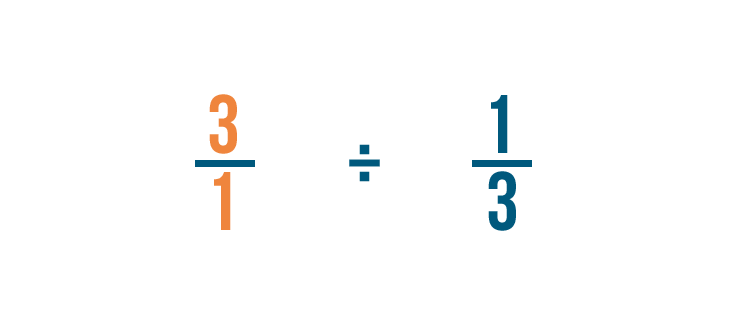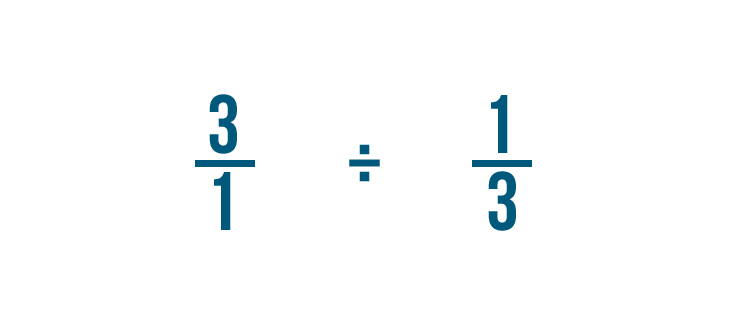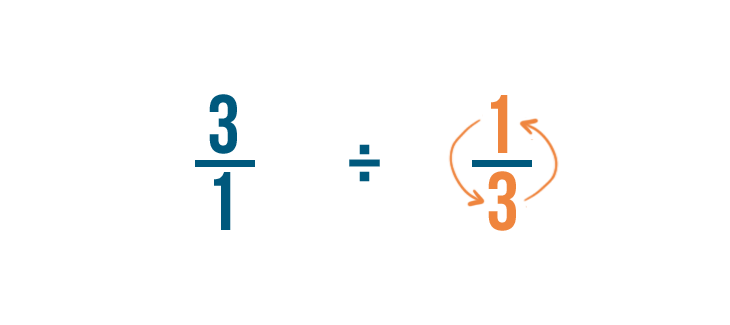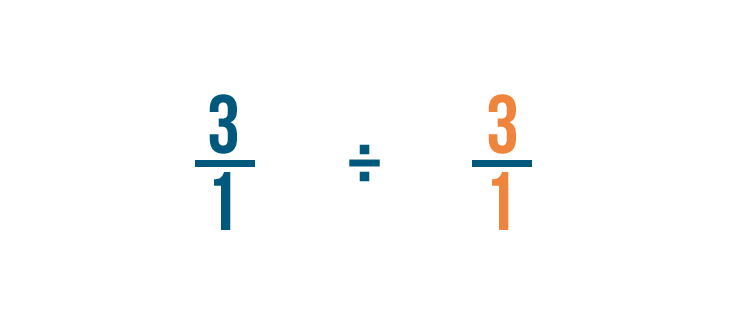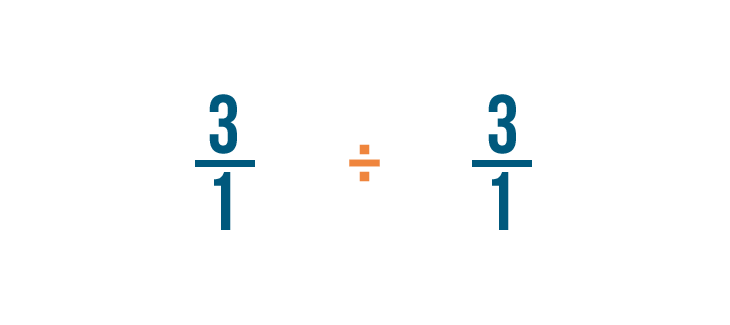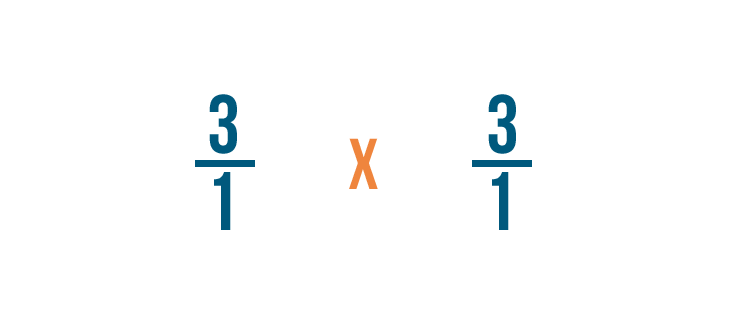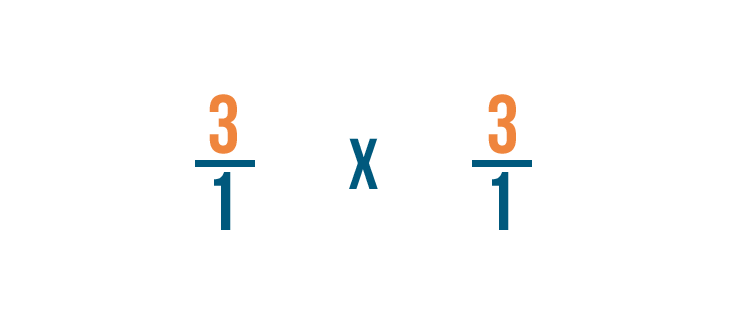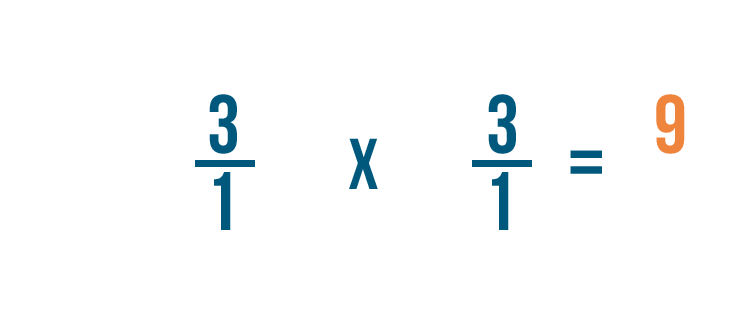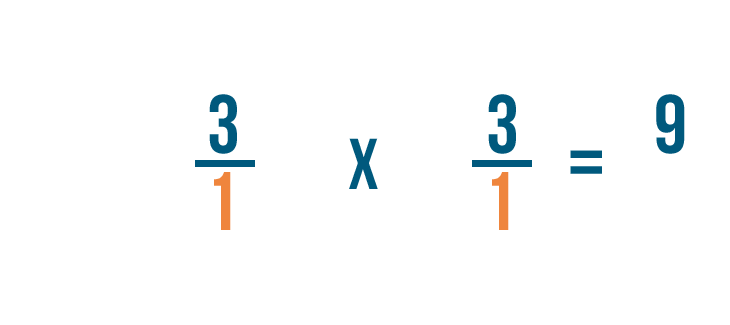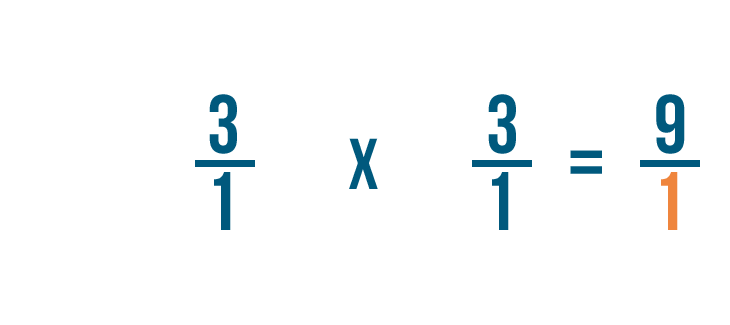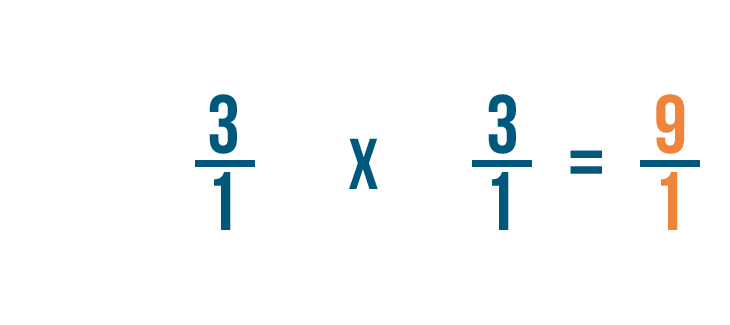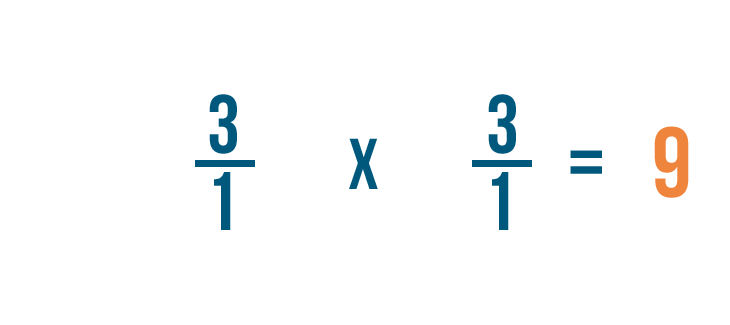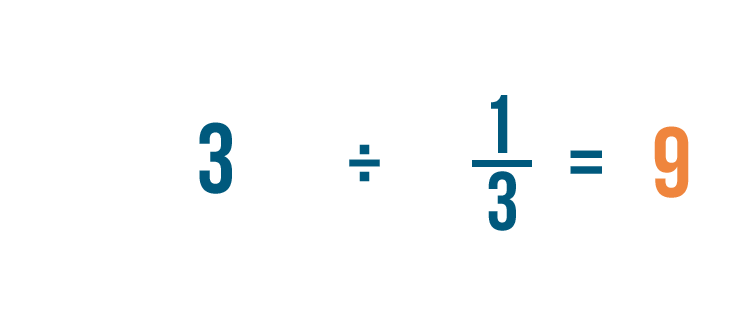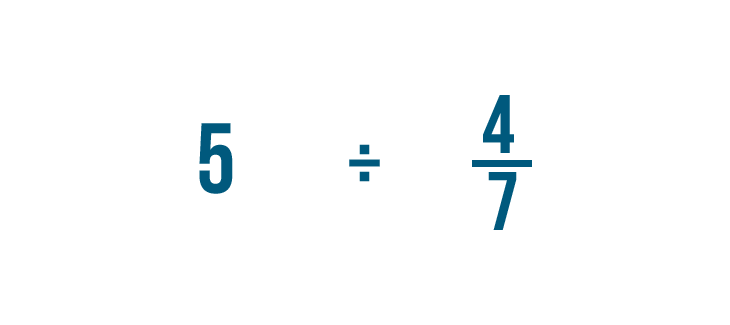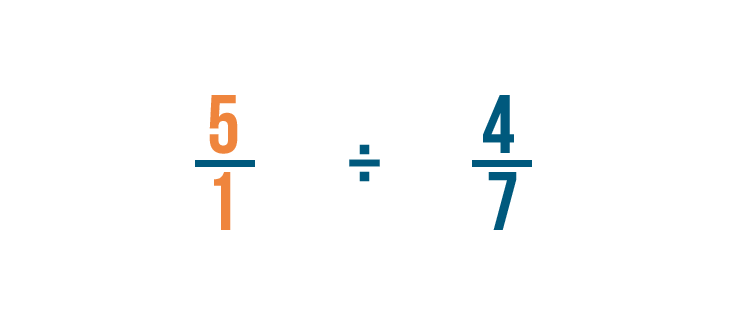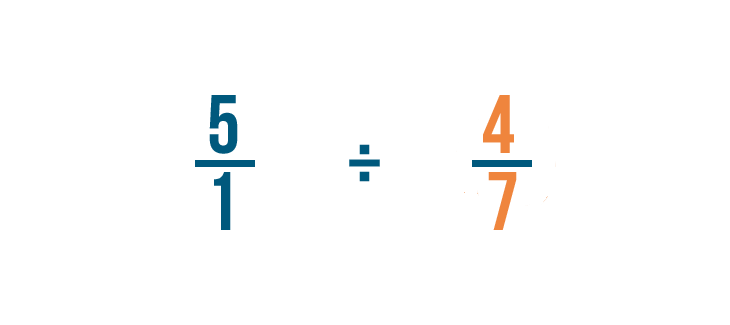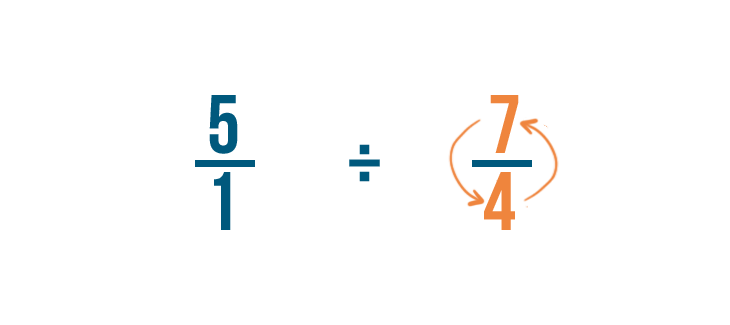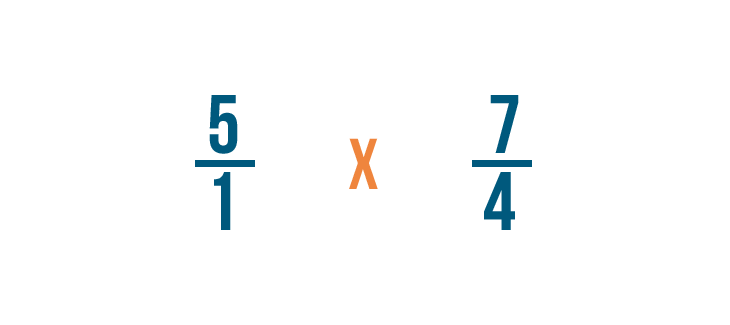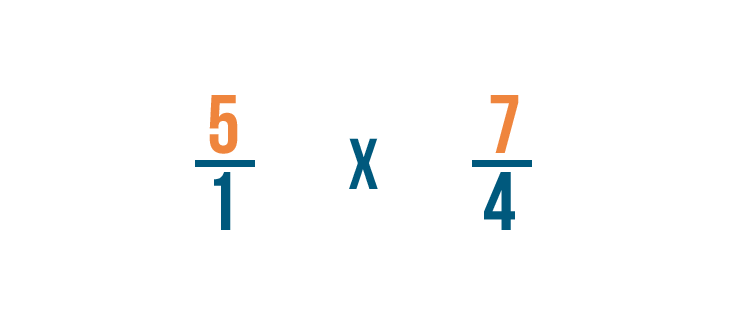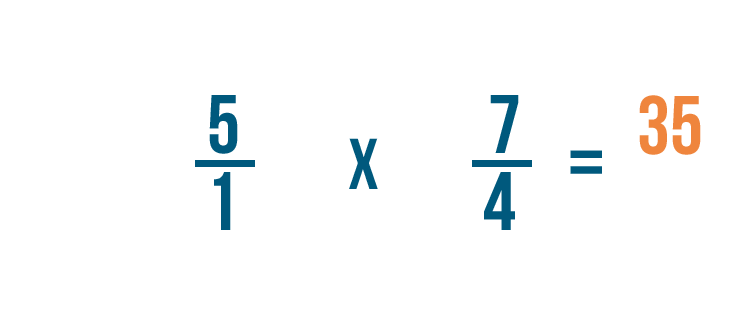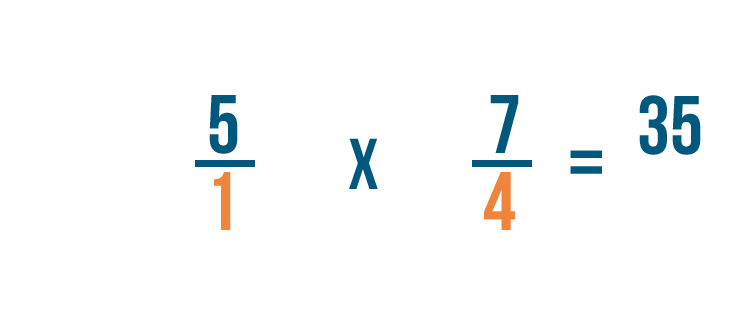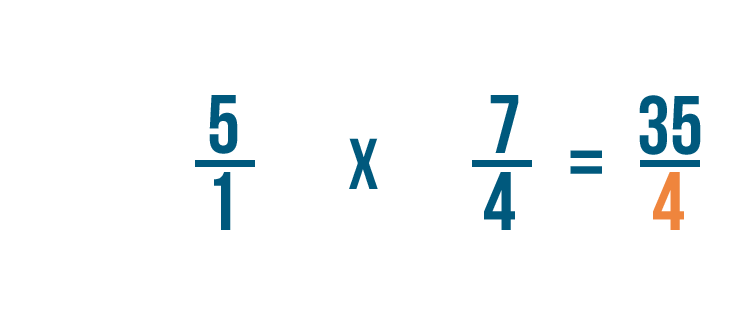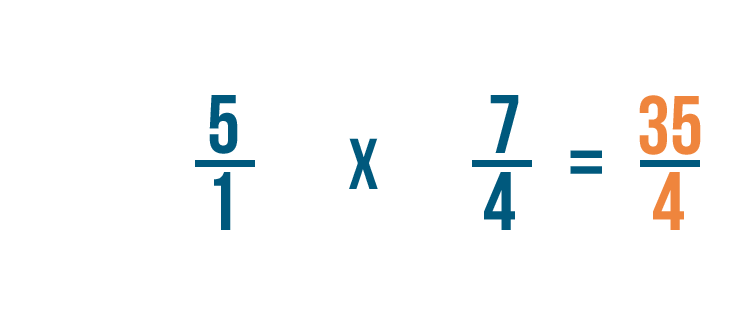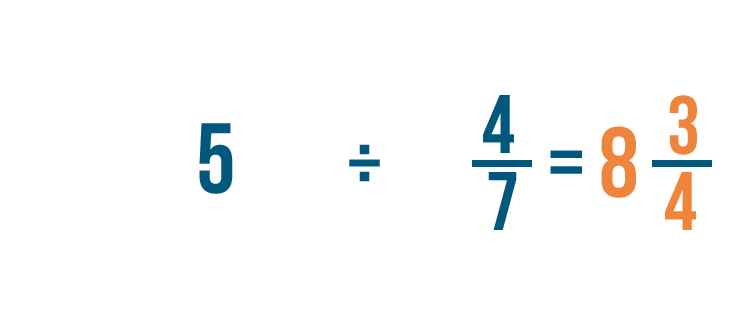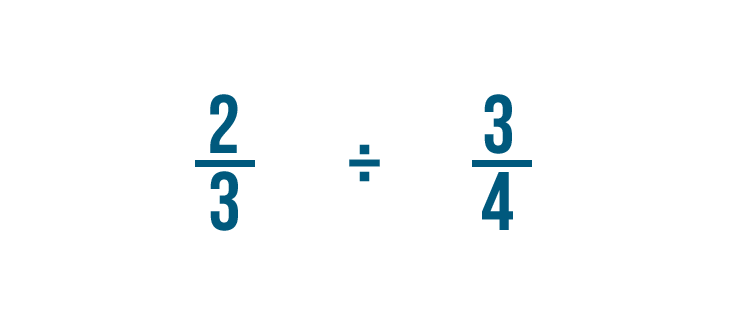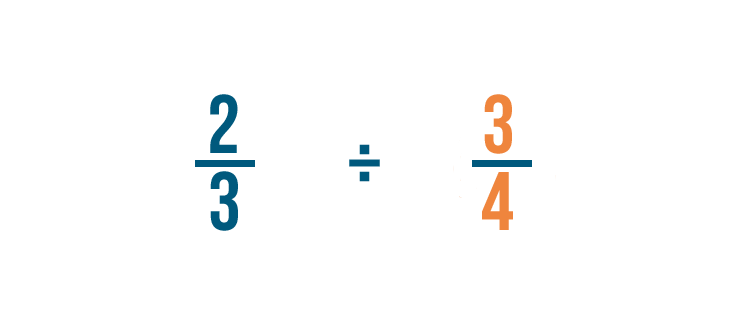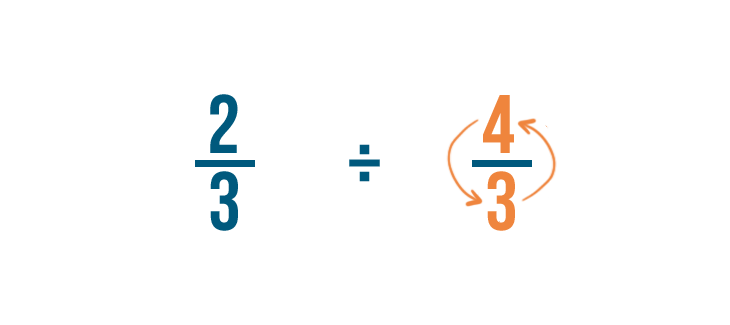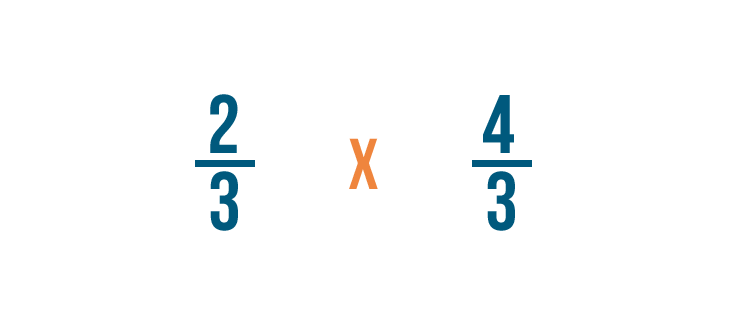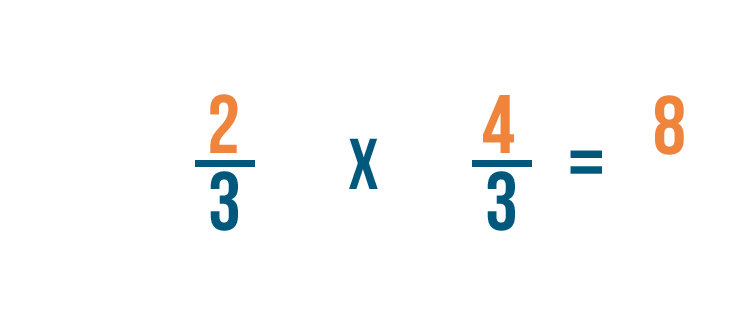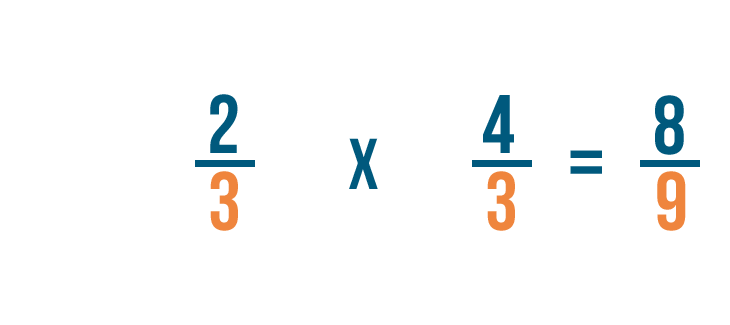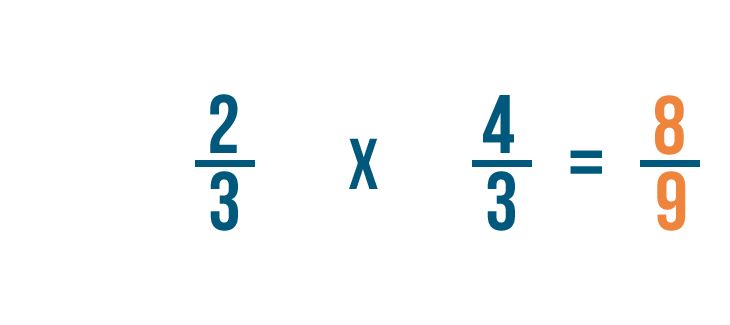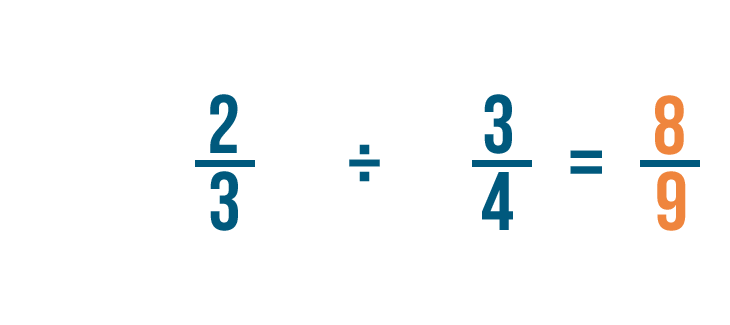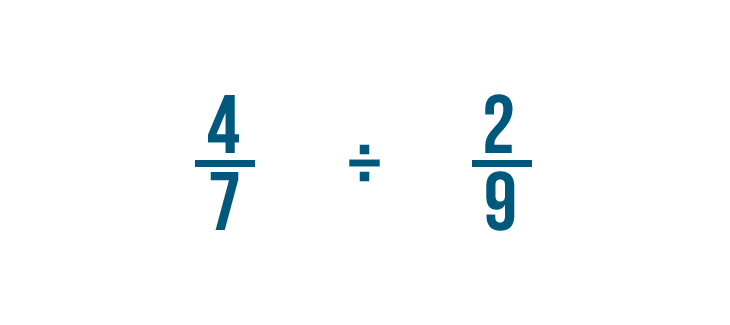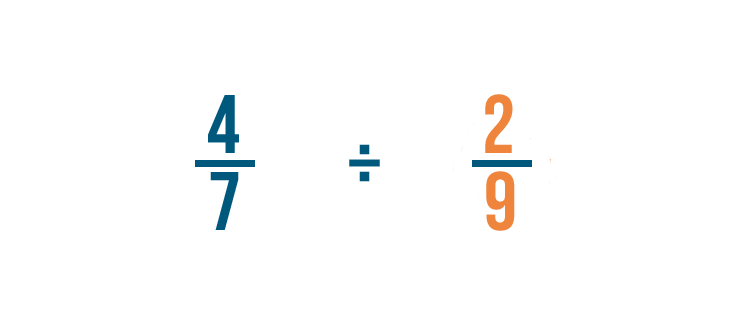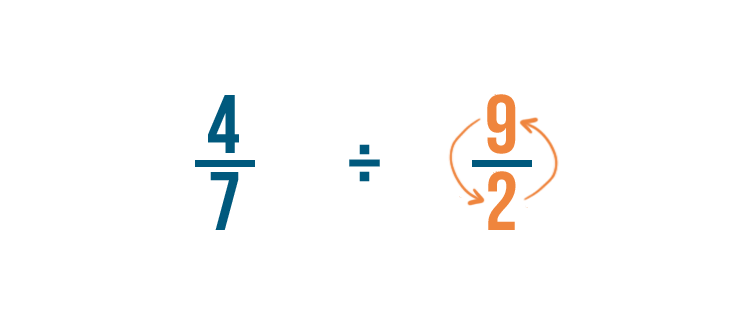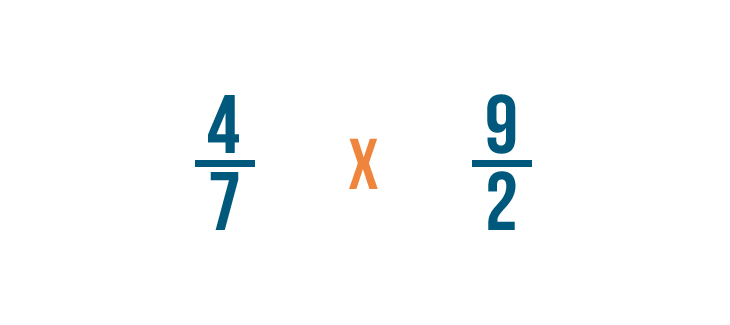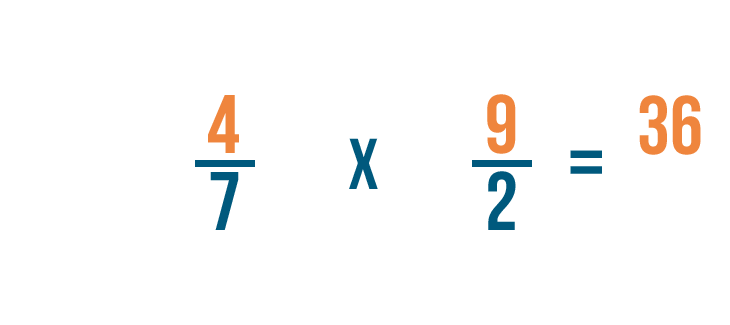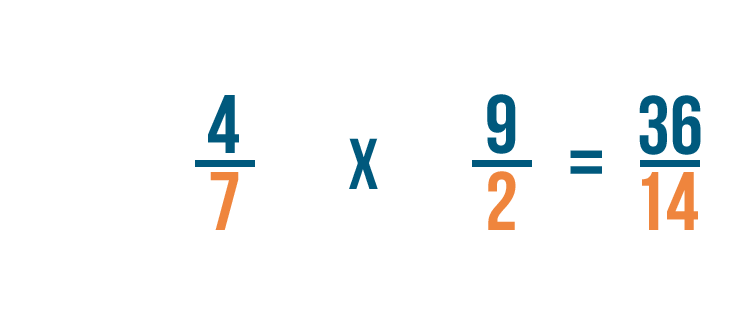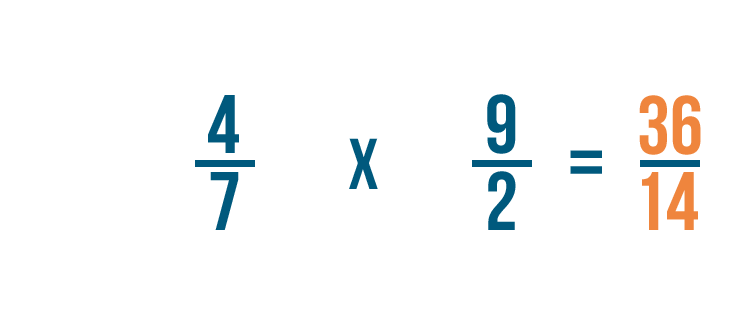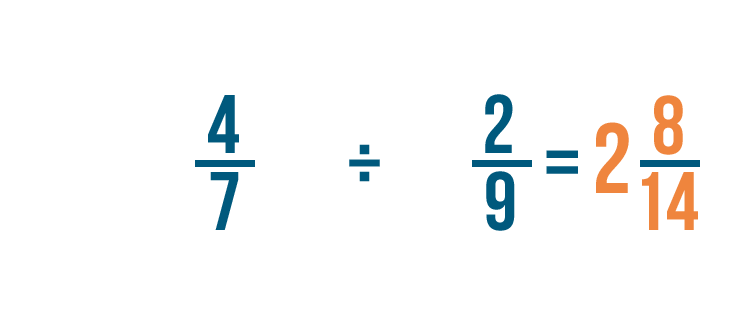Solving division problems with fractions
Now that we know how to write division problems, let's practice by solving a few. Dividing fractions is a lot like multiplying. It just requires one extra step. If you can multiply fractions, you can divide them too!
Click through the slideshow to learn how to divide a whole number by a fraction.
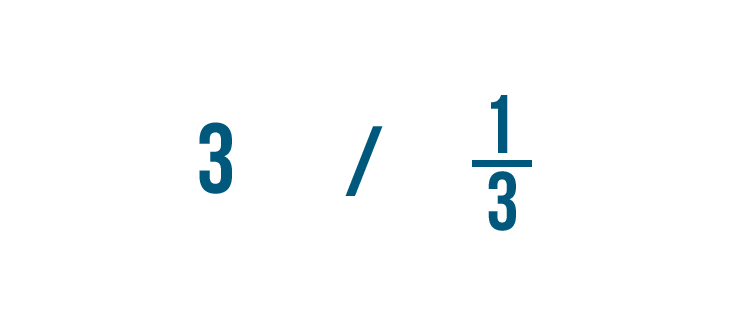
Let's divide 3 by 1/3. Remember, this is just another way to ask, "How many thirds are in 3?"
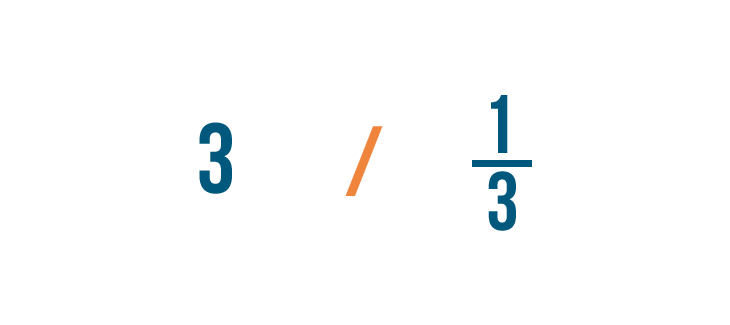
In our lesson on division, you learned how to write the division sign like this (/).
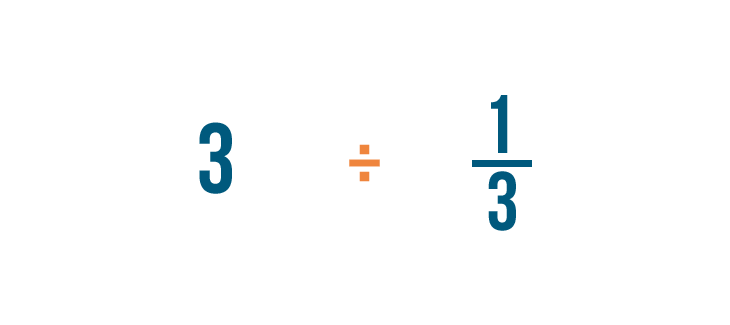
When dividing fractions, it will help to use the other symbol for division (÷) so we don't mistake it for a fraction.
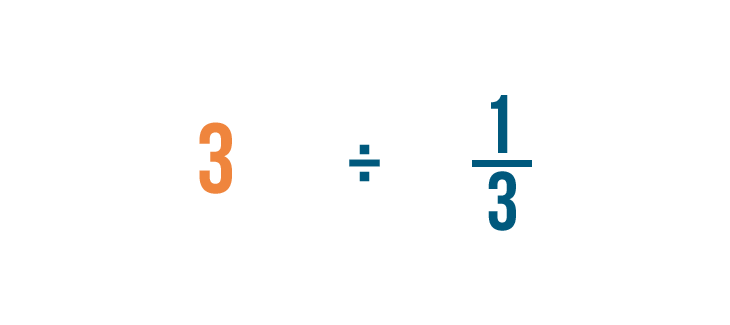
Just like multiplication, we'll start by looking for any whole numbers in our problem. There's one: 3.
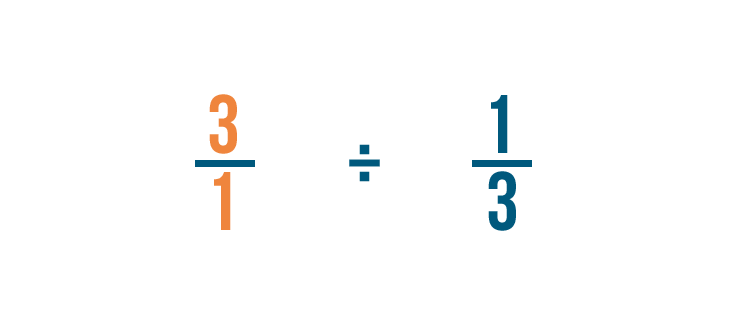
Remember, 3 is the same thing as 3/1.
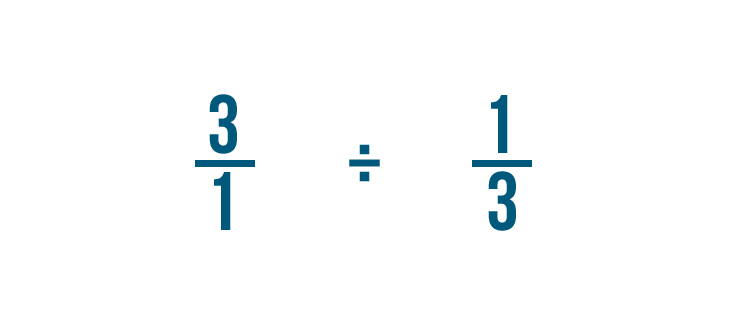
Before we can divide, we need to make one more change.
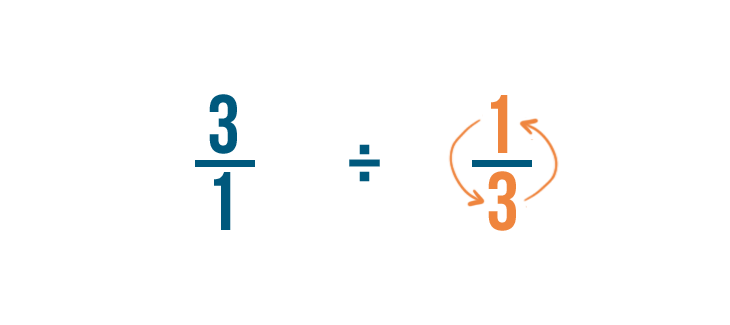
We'll switch the numerator and the denominator of the fraction we're dividing by: 1/3 in this example.
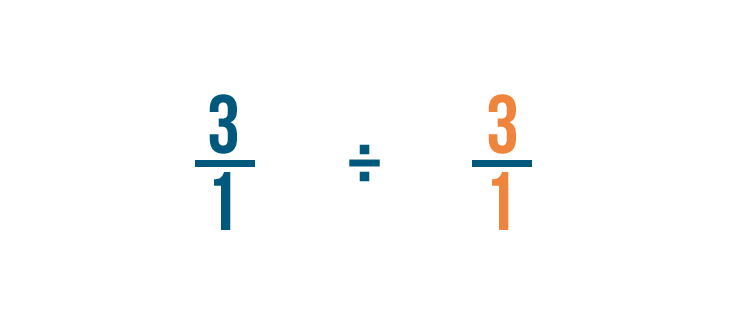
So 1/3 becomes 3/1.
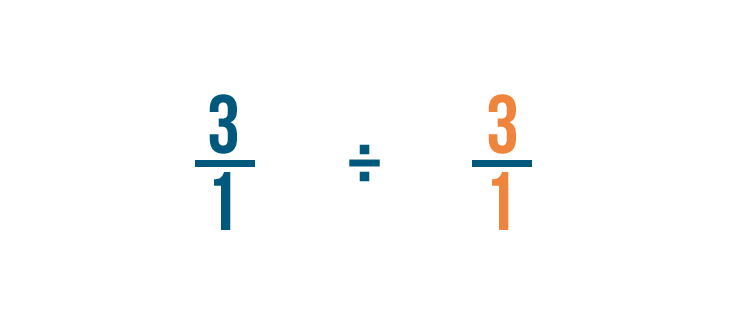
This is called finding the reciprocal, or opposite, of the fraction.
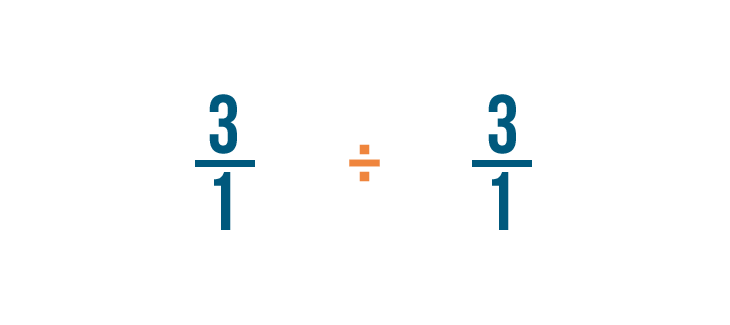
Since we're using the opposite of our original fraction, we'll also change the division sign (÷) to a multiplication sign (x).
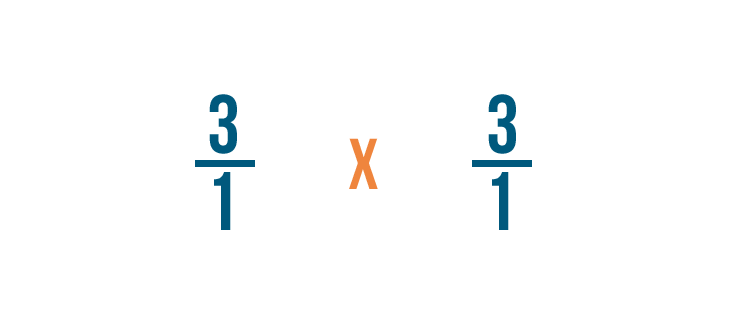
That's because multiplication is the opposite of division.
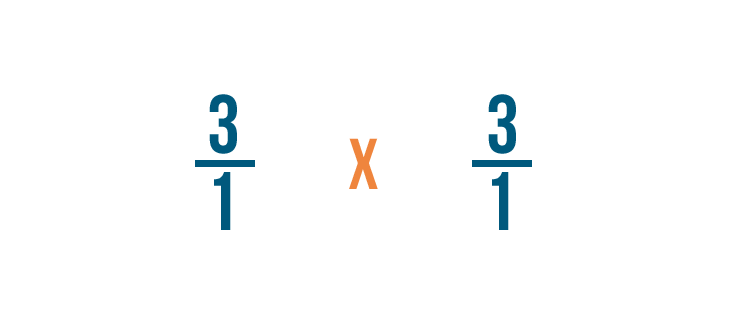
Now we can treat this like a regular multiplication problem.
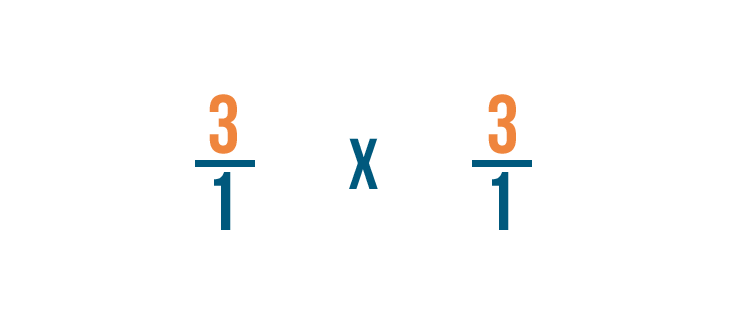
First, we'll multiply the numerators: 3 and 3.
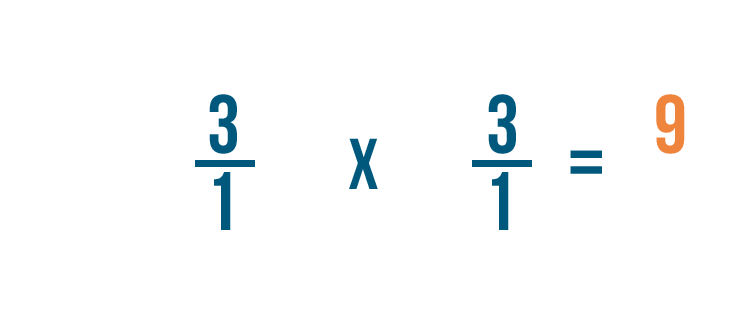
3 times 3 equals 9, so we'll write that next to the numerators.
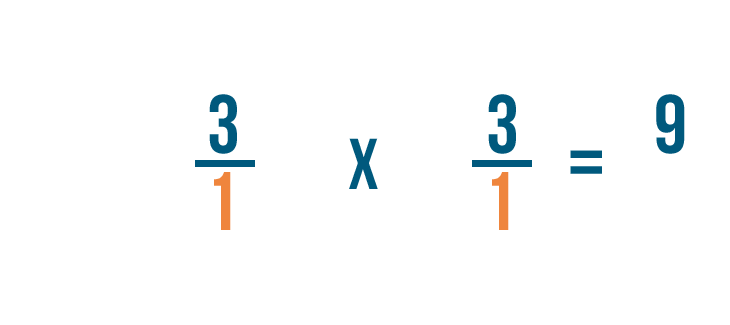
Next, we'll multiply the denominators: 1 and 1.
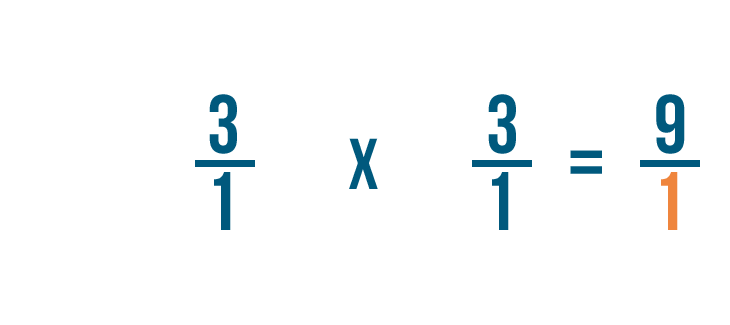
1 times 1 equals 1, so we'll write 1 next to the denominator.
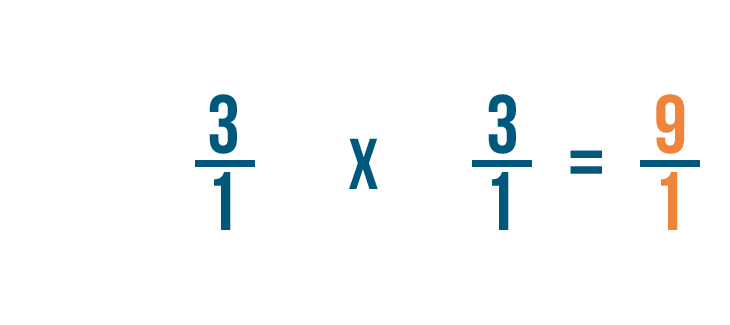
As you can see, 3/1 x 1/3 = 9/1.
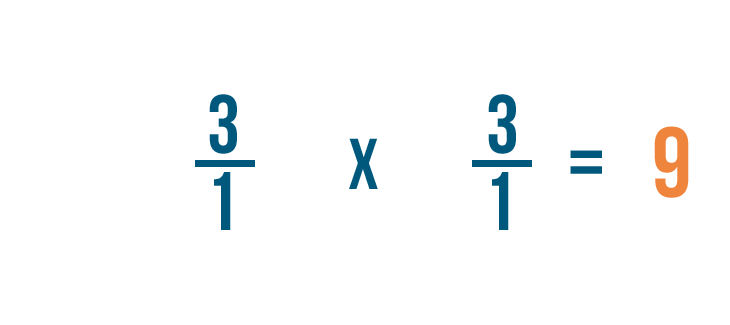
Remember, any fraction over 1 can also be expressed as a whole number. So 9/1 = 9.
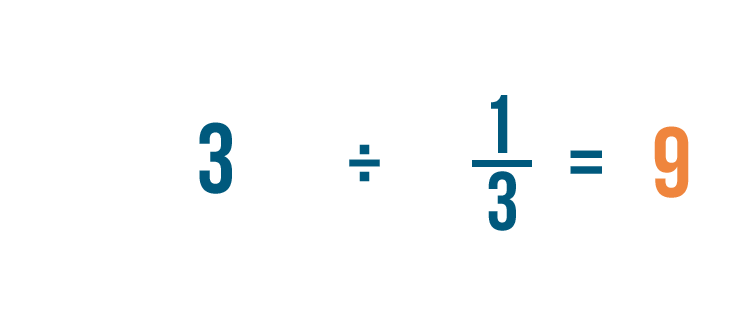
3 ÷ 1/3 = 9. In other words, there are 9 thirds in 3.
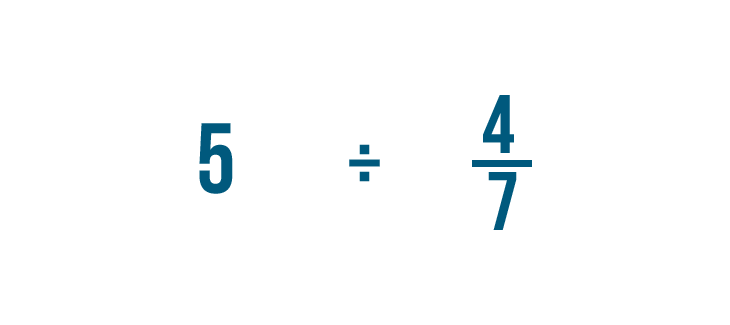
Let's try another example: 5 divided by 4/7.
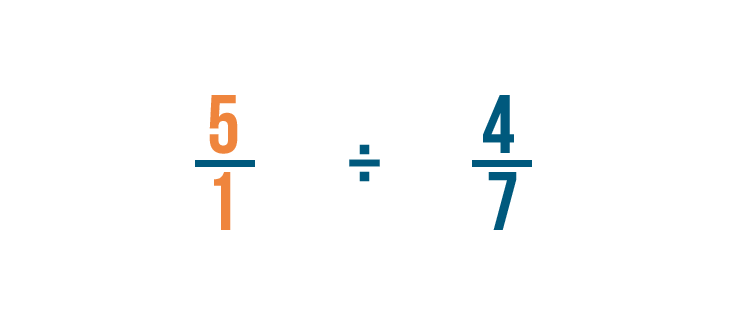
As always, we'll rewrite any whole numbers, so 5 becomes 5/1.
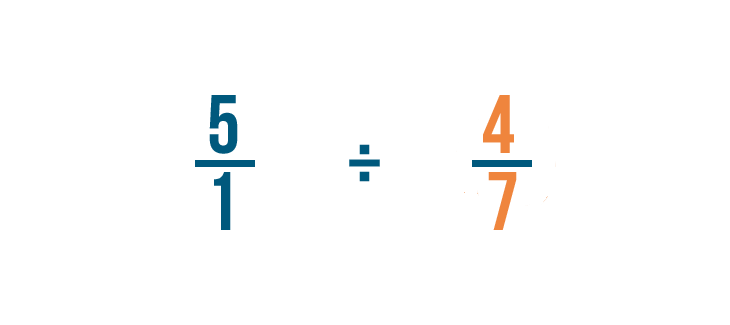
Next, we'll find the reciprocal of 4/7. That's the fraction we're dividing by.
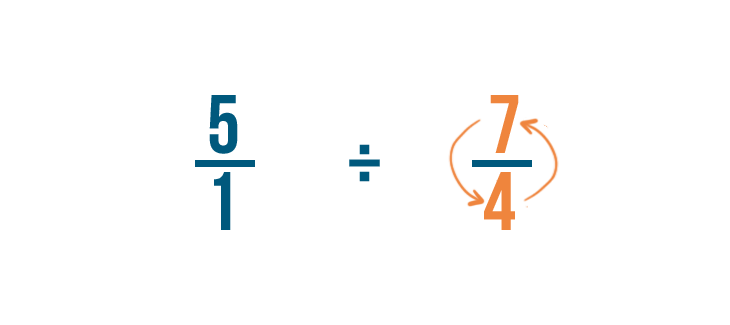
To do that, we'll switch the numerator and denominator, so 4/7 becomes 7/4.
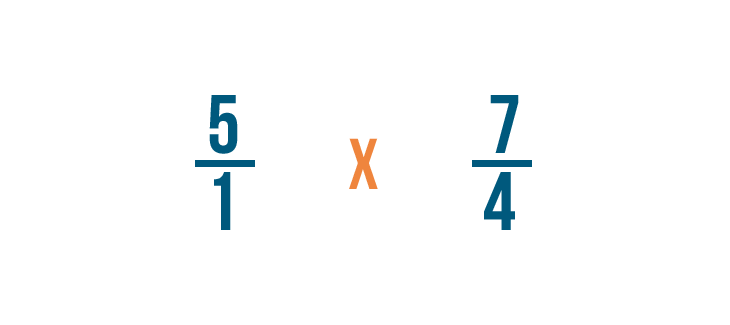
Then we'll change the division sign (÷) to a multiplication sign (x).
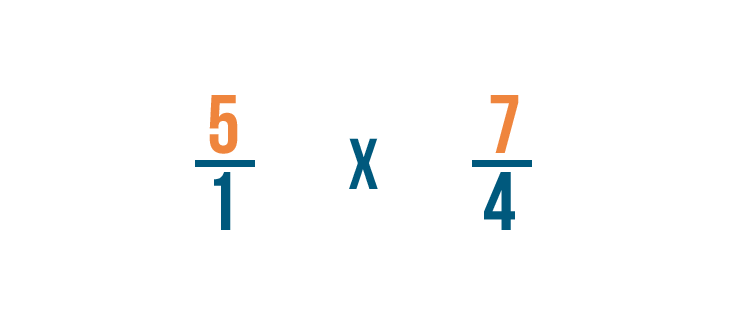
Now we can multiply as we normally would. First, we'll multiply the numerators: 5 and 7.
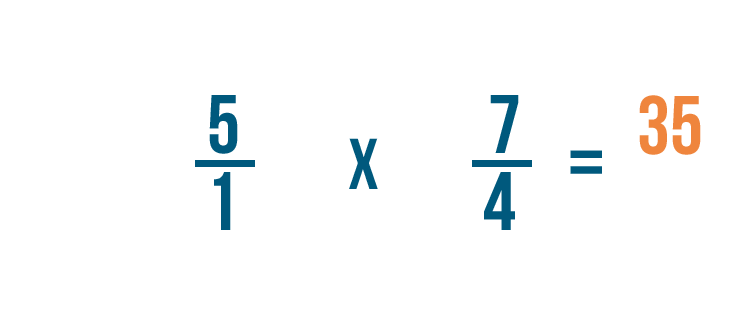
5 times 7 equals 35, so we'll write that next to the numerators.
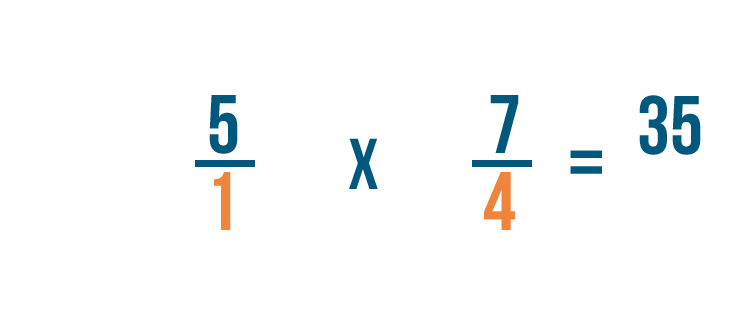
Next, we'll multiply the denominators: 1 and 4.
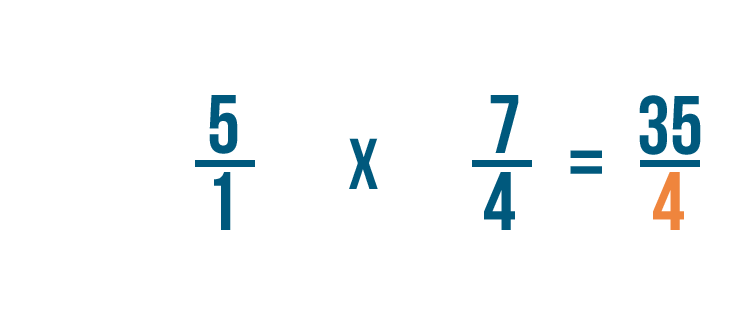
1 times 4 equals 4, so we'll write that next to the denominators.
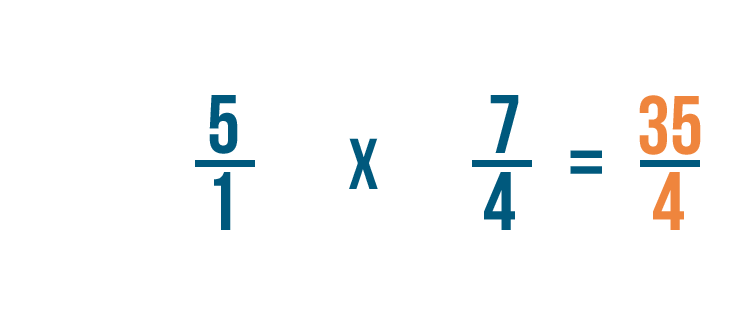
So 5/1 x 4/7 = 35/4.
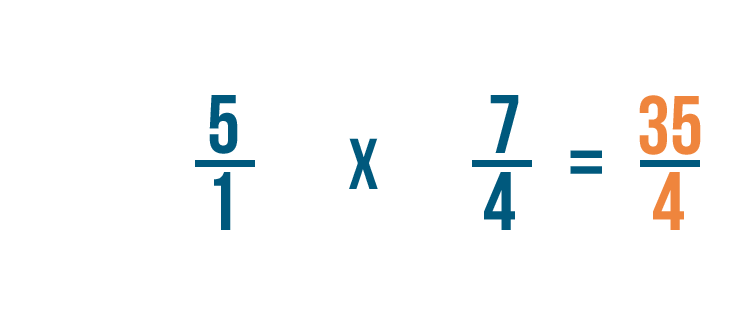
As you learned before, we could convert our improper fraction into a mixed number to make our answer easier to read.
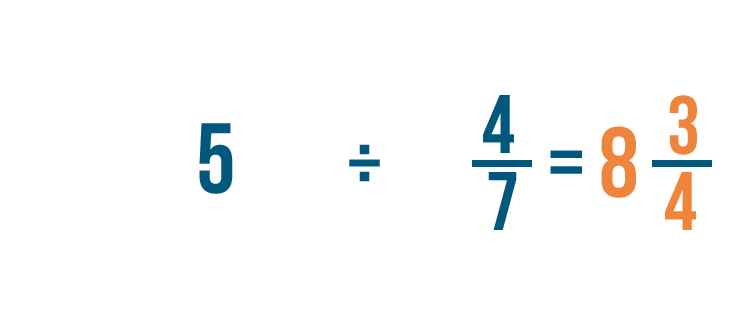
35/4 = 8 3/4. So 5 ÷ 4/7 = 8 3/4.

Now it's your turn! Try solving these division problems. Don't worry about reducing the answer for now.
Dividing two fractions
We just learned how to divide a whole number by a fraction. You can use the same method to divide two fractions.
Click through the slideshow to learn how to divide with two fractions.
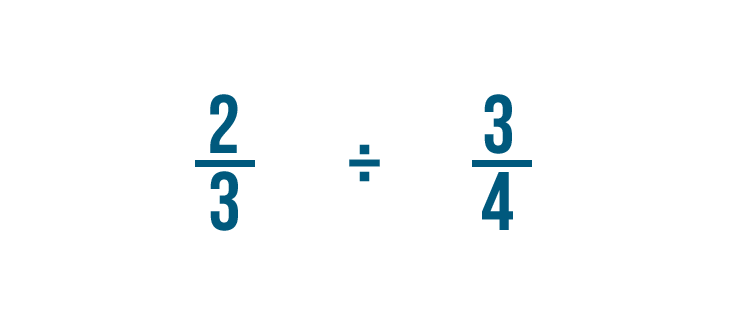
Let's try a problem with two fractions: 2/3 ÷ 3/4. Here, we want to know how many 3/4 are in 2/3.
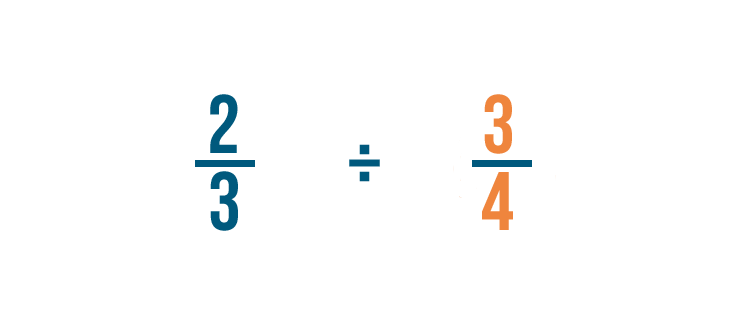
First, we'll find the reciprocal, or opposite, of the fraction we're dividing by: 3/4.
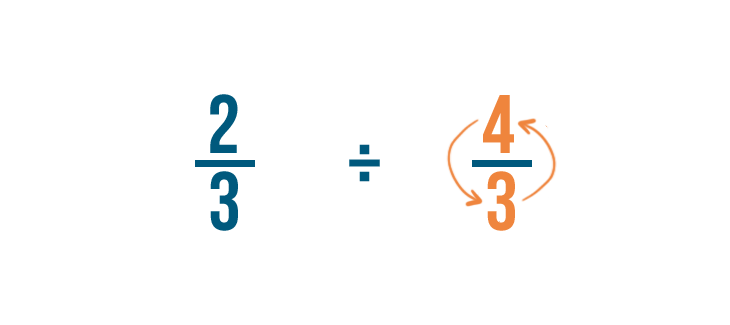
To do that, we'll switch the numerator and denominator. So 3/4 becomes 4/3.
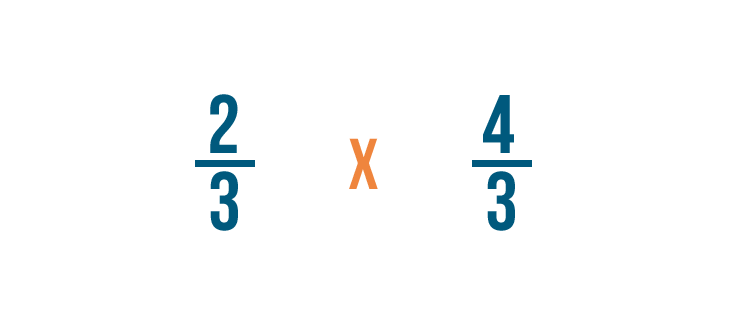
Next, we'll change the division sign (÷) to a multiplication sign (x).
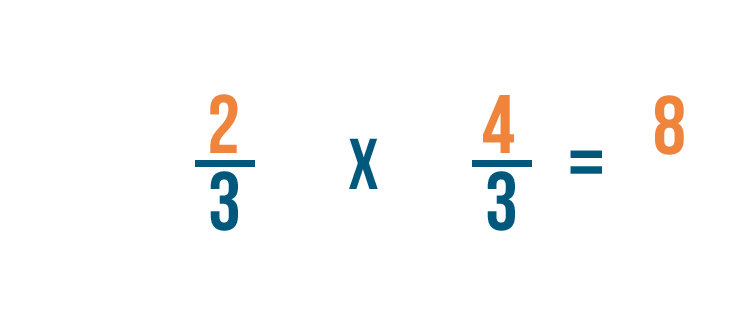
Now we'll multiply the numerators. 2 x 4 = 8, so we'll write 8 next to the top numbers.
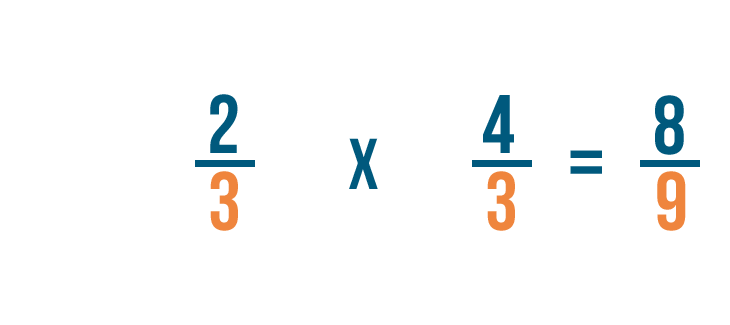
Next, we'll multiply the denominators. 3 x 3 = 9, so we'll write 9 next to the bottom numbers.
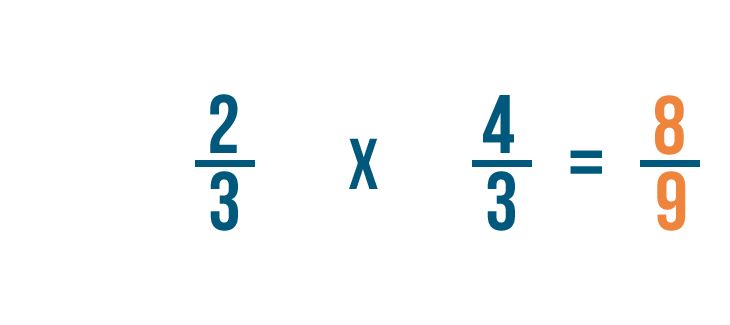
So 2/3 x 4/3 = 8/9.
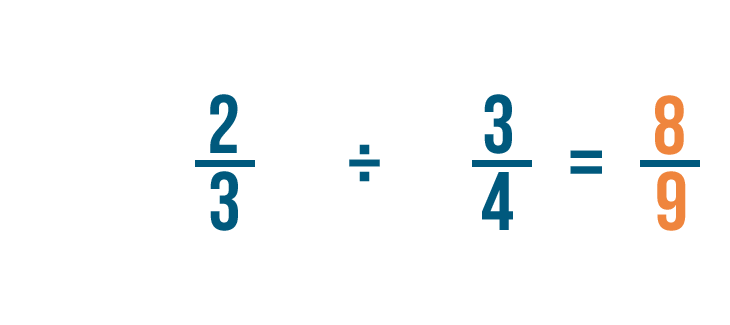
We could also write this as 2/3 ÷ 3/4 = 8/9.
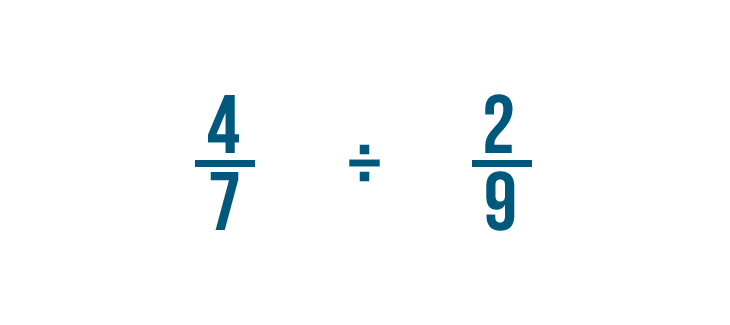
Let's try another example: 4/7 divided by 2/9.
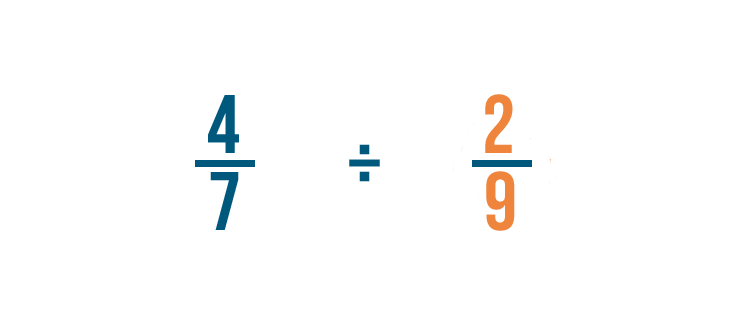
There are no whole numbers, so we'll find the reciprocal of the fraction we're dividing by. That's 2/9.
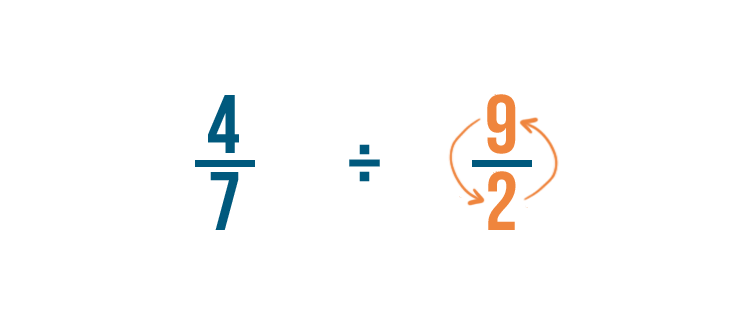
To do that, we'll switch the numerator and denominator. So 2/9 becomes 9/2.
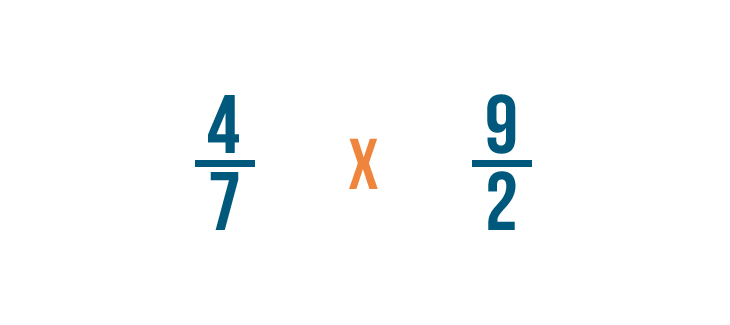
Now we'll change the division sign (÷) to a multiplication sign (x) and multiply as normal.
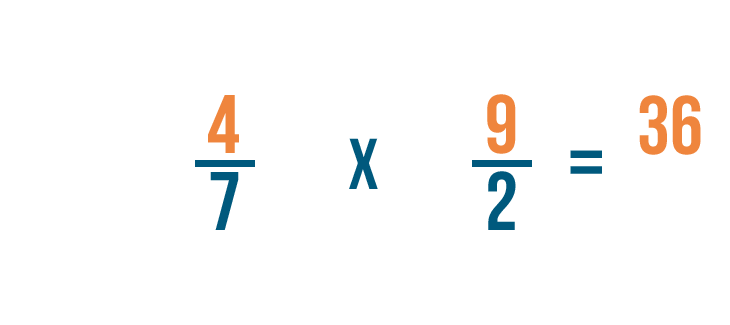
First, we'll multiply the numerators. 4 x 9 = 36.
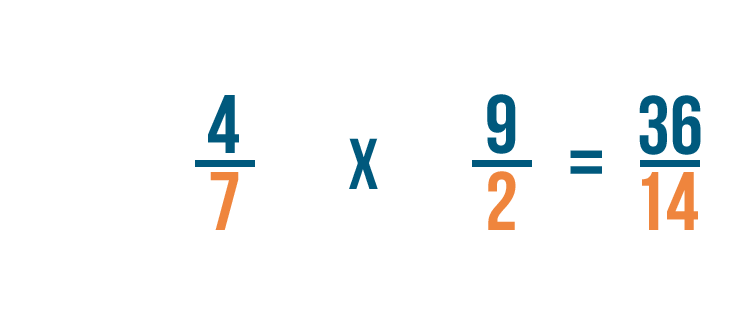
Next, we'll multiply the denominators. 7 x 2 = 14.
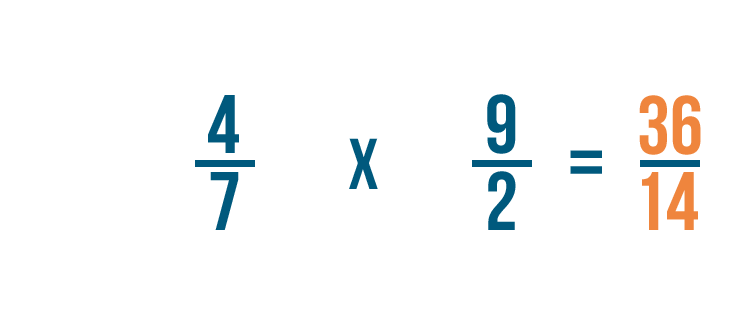
So 4/7 x 9/2 = 36/14. Just like before, you could convert this improper fraction into a mixed number.
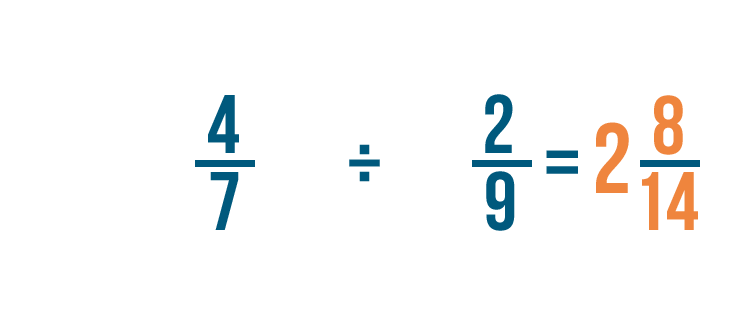
So 4/7 ÷ 2/9 = 2 8/14.

Now you try it! Try solving these division problems. Don't worry about reducing the answer for now.
Multiplying and dividing mixed numbers
How would you solve a problem like this?
As you learned in the previous lesson, whenever you're solving a problem with a mixed number you'll need to convert it into an improper fraction first. Then you can multiply or divide as usual.