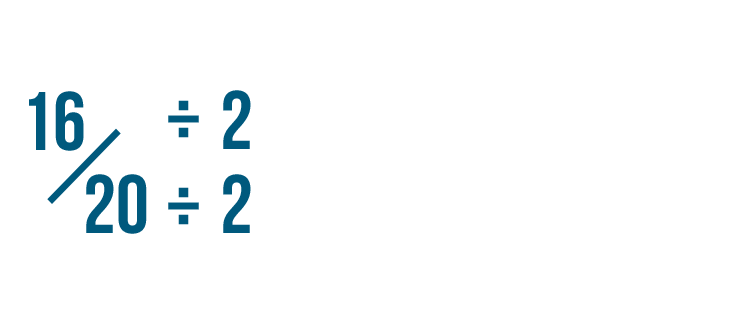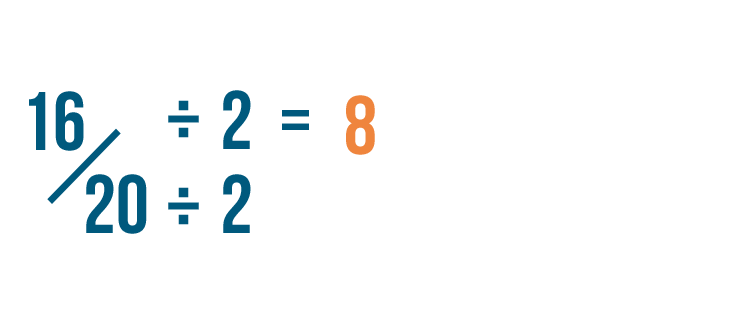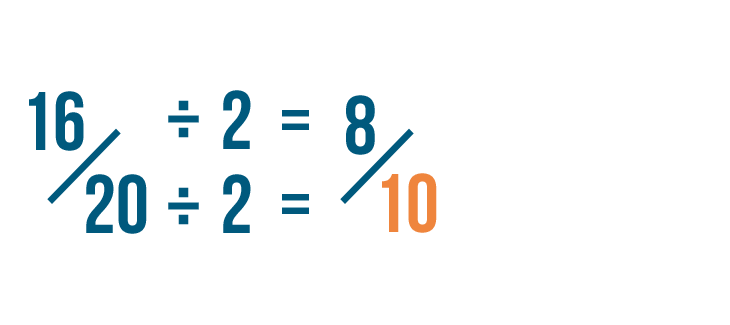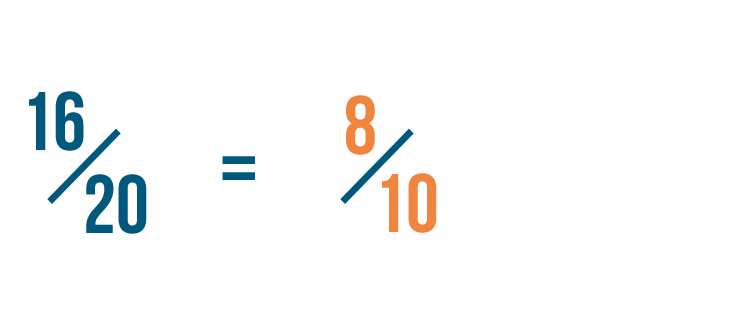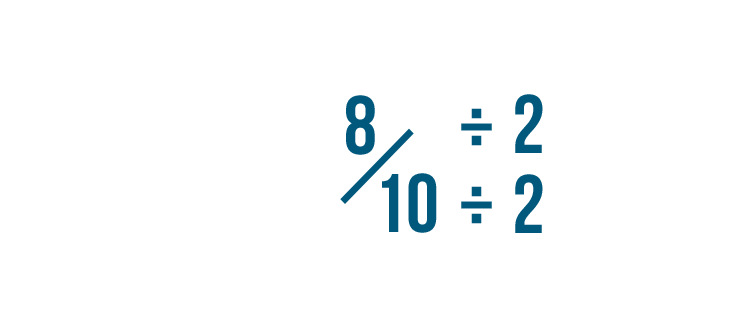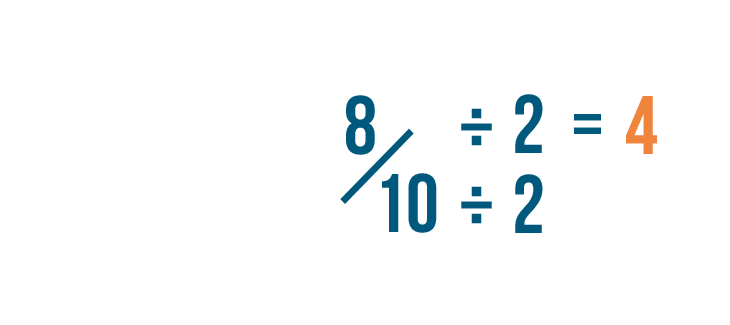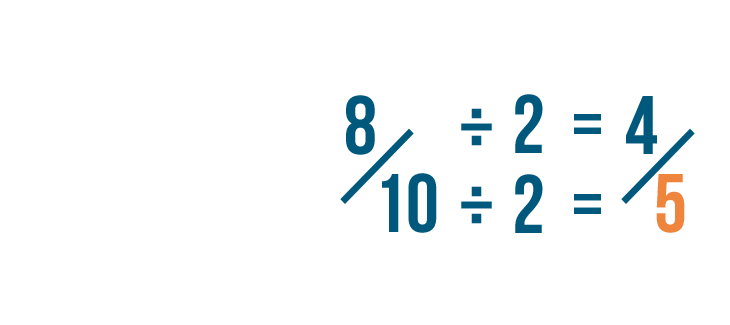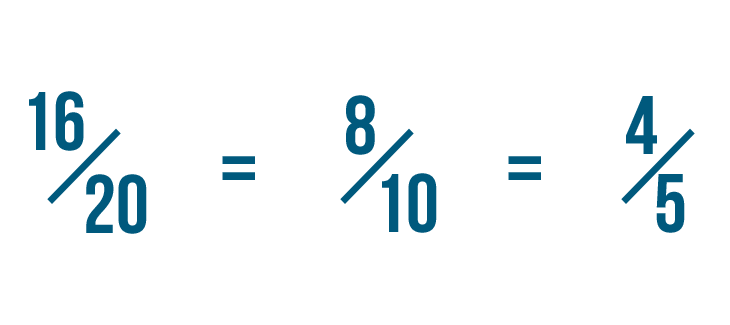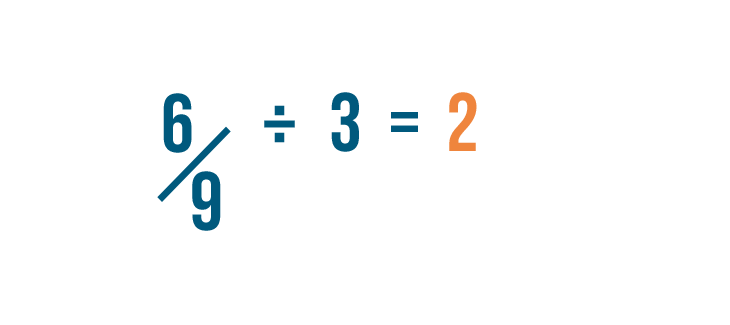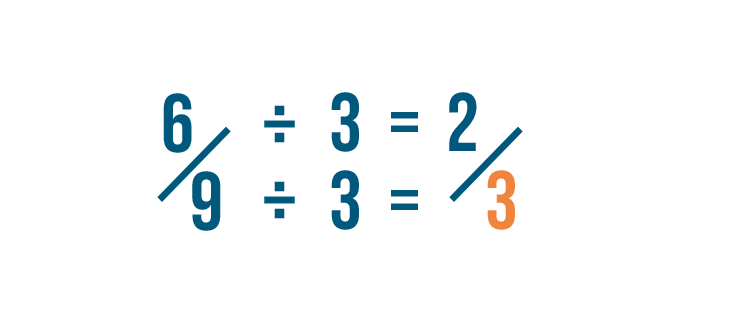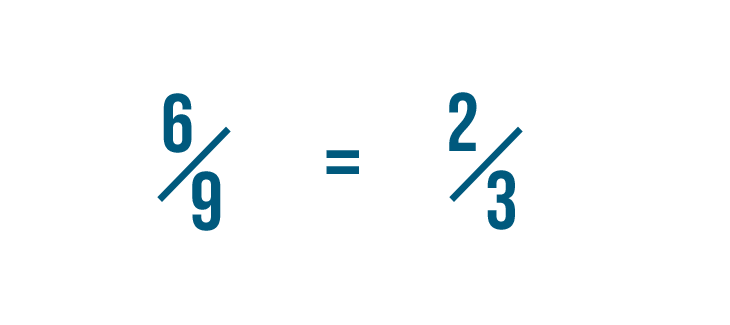Fractions
Comparing and Reducing Fractions
Reducing fractions
Which of these is larger: 4/8 or 1/2?

If you did the math or even just looked at the picture, you might have been able to tell that they're equal. In other words, 4/8 and 1/2 mean the same thing, even though they're written differently.
If 4/8 means the same thing as 1/2, why not just call it that? One-half is easier to say than four-eighths, and for most people it's also easier to understand. After all, when you eat out with a friend, you split the bill in half, not in eighths.
If you write 4/8 as 1/2, you're reducing it. When we reduce a fraction, we're writing it in a simpler form. Reduced fractions are always equal to the original fraction.
We already reduced 4/8 to 1/2. If you look at the examples below, you can see that other numbers can be reduced to 1/2 as well. These fractions are all equal.
5/10 = 1/2
11/22 = 1/2
36/72 = 1/2
These fractions have all been reduced to a simpler form as well.
4/12 = 1/3
14/21 = 2/3
35/50 = 7/10
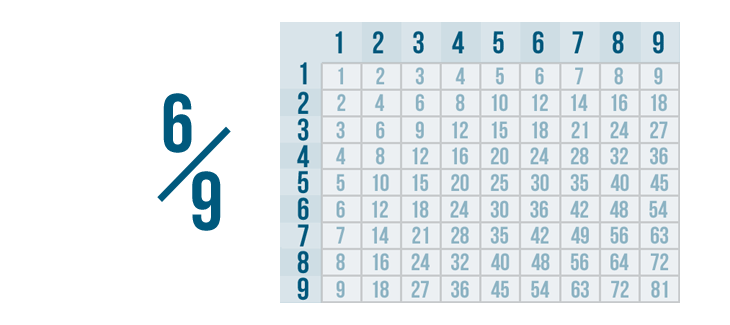
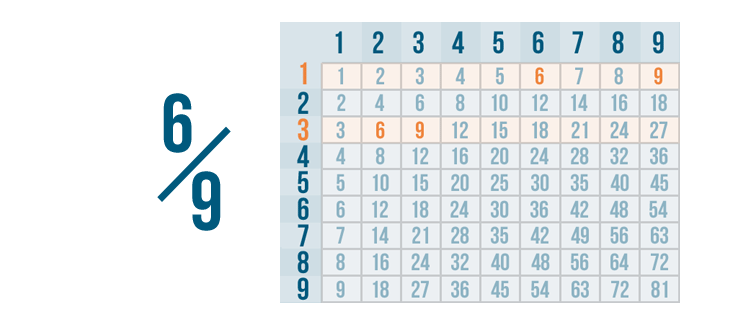
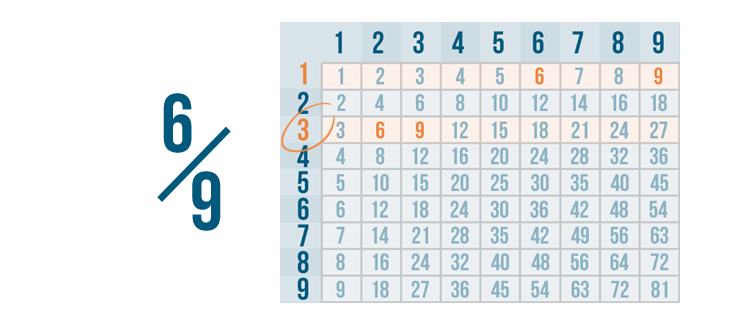
Click through the slideshow to learn how to reduce fractions by dividing.
Irreducible fractions
Not all fractions can be reduced. Some are already as simple as they can be. For example, you can't reduce 1/2 because there's no number other than 1 that both 1 and 2 can be divided by. (For that reason, you can't reduce any fraction that has a numerator of 1.)
Some fractions that have larger numbers can't be reduced either. For instance, 17/36 can't be reduced because there's no number that both 17 and 36 can be divided by. If you can't find any common multiples for the numbers in a fraction, chances are it's irreducible.
Now you try it! Reduce each fraction to its simplest form.